江西省吉安市遂川县2021-2022学年七年级下学期期末数学...

更新时间：2024-07-13 浏览次数：73 类型：期末考试

一、单选题

1. (2022七下·遂川期末) 计算 $\text{[math]}$ 所得结果为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022七下·遂川期末) 下列是北京大学，中国科学院，中国医科大学和中国人民公安大学的标志中的图案，其中是轴对称图形的有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2022七下·遂川期末) 如图所示，在所标识的角中，内错角是（　　）

A . $\text{[math]}$ 和 $\text{[math]}$ B . $\text{[math]}$ 和 $\text{[math]}$ C . $\text{[math]}$ 和 $\text{[math]}$ D . $\text{[math]}$ 和 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·合肥期中) 下列不能用平方差公式计算的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·遂川期末) 如图，某市夏天的温度随时间变化的图象，通过观察可知，下列说法中错误的是（　　）

A . 这天15时温度最高 B . 这天3时温度最低 C . 这天最高温度与最低温度的差是 $\text{[math]}$ D . 这天0～3时，15～24时温度在下降

答案解析收藏纠错 + 选题
6. (2022七下·遂川期末) 如图1，将1个长方形沿虚线剪开得到两个长方形，再将这两个长方形拼成图2，则下列等式可以解释两图形面积变化的数量关系的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2022七下·遂川期末) 若 $\text{[math]}$ 与 $\text{[math]}$ 互为邻补角，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
8. (2022七下·遂川期末) 甲型 $\text{[math]}$ 流感在墨西哥爆发并在全球蔓延，研究表明，甲型 $\text{[math]}$ 流感球型病毒细胞的直径约为 $\text{[math]}$ ，用科学记数法表示这个数是m．

答案解析收藏纠错 + 选题
9. (2022七下·遂川期末) 如图，三角形ABC的高AD=4，BC=6，点E在BC上运动，若设BE的长为 $\text{[math]}$ 三角形ACE的面积为有y，则y与x的关系式为.

答案解析收藏纠错 + 选题
10. (2022七下·遂川期末) 一副直角三角板如图放置，点D在边 $\text{[math]}$ 上，点F在 $\text{[math]}$ 的延长线上， $\text{[math]}$ ，则 $\text{[math]}$ 的余角的度数为度．

答案解析收藏纠错 + 选题
11. (2022八上·吉安开学考) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2022八上·吉安开学考) 如图，一幅三角板的两个直角顶点重合，已知 $\text{[math]}$ ， $\text{[math]}$ ，则当 $\text{[math]}$ 的一边与 $\text{[math]}$ 的一边平行或重合，且点C在 $\text{[math]}$ 的左侧时， $\text{[math]}$ （小于平角）的度数为．

答案解析收藏纠错 + 选题

三、解答题

13. (2022七下·遂川期末)
1. （1）计算： $\text{[math]}$ ；
2. （2）如图所示， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 比 $\text{[math]}$ 大 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
14. (2022七下·遂川期末) 为了有效提高人民免疫水平，最终阻断病毒传染，某地接种新冠疫苗，已知每天可接种800人．
1. （1）直接写出接种人数y与时间x（天）之间的函数关系式；
2. （2）如果计划接种6.4万人，则需要多天才能完成接种任务？
答案解析收藏纠错 + 选题
15. (2022七下·遂川期末) 先化简，再求值： $\text{[math]}$ ，其中a=﹣3，b= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024七下·井冈山期末) 一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出1个球是红球的概率为 $\text{[math]}$ ．
1. （1）求口袋中黄球的个数；
2. （2）现规定：摸到红球得5分，摸到黄球得3分，摸到蓝球得2分（每次摸后放回），乙同学在一次摸球游戏中，第一次随机摸到一个红球第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学三次摸球所得分数之和不低于10分的概率．
答案解析收藏纠错 + 选题
17. (2022七下·遂川期末) 如图，在所标注的角中．
1. （1）对顶角有对，邻补角有对；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题

18. (2023七下·市北区期末) 某公交车每月的支出费用为4000元，每月的乘车人数x(人)与每月利润(利润＝收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的)：

x(人)	500	1000	1500	2000	2500	3000	…
y(元)	﹣3000	﹣2000	﹣1000	0	1000	2000	…

（1）在这个变化过程中，是自变量，是因变量；
（2）观察表中数据可知，每月乘客量达到人以上时，该公交车才不会亏损；
（3）请你估计当每月乘车人数为3500人时，每月利润为多少元？

答案解析收藏纠错 + 选题

19. (2022七下·遂川期末) 把推理过程补充完整，并填写相应的理由．
如图，∵AC∥EF（已知），
∴ $\text{[math]}$ ．（        ）
$\text{[math]}$ ．（        ）
又∵ $\text{[math]}$ 平分 $\text{[math]}$ （已知），
∴ $\text{[math]}$       ▲       ．（        ）
∴ $\text{[math]}$ ．（        ）

答案解析收藏纠错 + 选题
20. (2022七下·遂川期末)
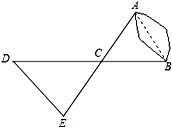
如图，A、B两点分别位于一个池塘的两侧，池塘西边有一座假山D，在DB的中点C处有一个雕塑，小川从点A出发，沿直线AC一直向前经过点C走到点E，并使CE＝CA，然后他测量点E到假山D的距离，则DE的长度就是A、B两点之间的距离．
1. （1）你能说明小川这样做的根据吗？
2. （2）如果小川恰好未带测量工具，但是知道A和假山D、雕塑C分别相距200米、120米，你能帮助他确定AB的长度范围吗？
答案解析收藏纠错 + 选题
21. (2022七下·遂川期末) 如图，将两个长方形用不同方式拼成图1和图2两个图形．
1. （1）若图1中的阴影部分面积为 $\text{[math]}$ ，则图2中的阴影部分面积为（用含字母a，b的代数式表示）；
2. （2）由（1）你可以得到的等式是；
3. （3）根据你所得到的等式解决下面的问题：
  ①若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；
  
  ②计算： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2022七下·遂川期末) 观察下列运算过程：
$\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$ ， …
1. （1）根据以上运算过程和结果，我们发现： $\text{[math]}$ ； $\text{[math]}$ ；
2. （2）仿照（1）中的规律，判断 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系；
3. （3）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2022七下·遂川期末) 如图，在 $\text{[math]}$ ABC中，∠ACB＝90°，AC＝BC，AB＝8cm，过点C作射线CD，且CD∥AB，点P从点C出发，沿射线CD方向匀速运动，速度为3cm/s；点Q从点A出发，沿AB边向点B匀速运动，速度为1cm/s，当点Q停止运动时，点P也停止运动．连接PQ，CQ，设动点的运动时间为t（s）（0＜t＜8），解答下列问题：
1. （1）用含有t的代数式表示CP和BQ的长度；
2. （2）当t＝2时，请说明PQ∥BC；
3. （3）设 $\text{[math]}$ 的面积为S（cm²），求S与t之间的关系式．
答案解析收藏纠错 + 选题