人教版九年级上对接中考知识点复习专项计划——二次函数的应用之...

更新时间：2022-09-26 浏览次数：71 类型：复习试卷

一、单选题

1. (2019九上·文登期中) 某民俗旅游村为接待游客住宿需要，开设了有100张床位的旅馆．当每张床位每天收费100元时，床位可全部租出．若每张床位每天收费提高20元，则相应地减少了10张床位租出．如果每张床位每天以20元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是（）

A . 140元 B . 150元 C . 160元 D . 180元

答案解析收藏纠错 + 选题

二、填空题

2. 某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a元（a＞0）。未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元。通过市场调研发现，该时装单价每降1元，每天销量增加4件。在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t（t为正整数）的增大而增大，a的取值范围应为。

答案解析收藏纠错 + 选题
3. 数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件）
100
110
120
130
…
月销量（件）
200
180
160
140
…
已知该运动服的进价为每件60元，设售价为x（x≥100）元，则月销量是件，销售该运动服的月利润为元（用含x的式子表示）.

答案解析收藏纠错 + 选题
4. 某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件，当每件的定价为元时，该服装店平均每天的销售利润最大．

答案解析收藏纠错 + 选题

三、综合题

5. (2018九上·山东期中) 某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系：y=-x+60(30≤x≤60)．设这种双肩包每天的销售利润为w元．
1. （1）求w与x之间的函数关系式；
2. （2）这种双肩包销售单价定为多少元时，每天的销售利润最大?最大利润是多少元?
3. （3）如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元?
答案解析收藏纠错 + 选题
6. (2019九上·淅川期末) 某商店将每件进价为80元的某种商店按每件110元出售，每天可售出100件．该商店想通过降低售价、增加销售量的方法来提高利润．经市场调查，发现这种商品每件每降价5元，每天的销售量可增加50件．设商品降价x元，每天销售该商品获得的利润为y元．
1. （1）求y（元）关于x（元）的函数关系式，并写出x的取值范围．
2. （2）求当x取何值时y最大？并求出y的最大值．
3. （3）若要是每天销售利润为3750元，且尽可能最大的向顾客让利，应将该商品降价多少元？
答案解析收藏纠错 + 选题
7. (2020·抚州模拟) 我市“佳禾”农场的十余种有机蔬菜在北京市场上颇具竞争力．某种有机蔬菜上市后，一经销商在市场价格为10元/千克时，从“佳禾”农场收购了某种有机蔬菜2000 千克存放入冷库中．据预测，该种蔬菜的市场价格每天每千克将上涨0.2元，但冷库存放这批蔬菜时每天需要支出各种费用合计148元，已知这种蔬菜在冷库中最多保存90天，同时，平均每天将会有6千克的蔬菜损坏不能出售．
1. （1）若存放x天后，将这批蔬菜一次性出售，设这批蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．
2. （2）经销商想获得利润7200元，需将这批蔬菜存放多少天后出售？（利润=销售总金额﹣收购成本﹣各种费用）
3. （3）经销商将这批蔬菜存放多少天后出售可获得最大利润？最大利润是多少？
答案解析收藏纠错 + 选题
8. 某快餐店试销某种套餐，试销一段时间后发现，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店每天的利润．
1. （1）若每份套餐售价不超过10元．
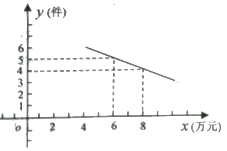
  ①试写出y与x的函数关系式；
  ②若要使该店每天的利润不少于800元，则每份套餐的售价应不低于多少元？
2. （2）该店把每份套餐的售价提高到10元以上，每天的利润能否达到1560元？若能，求出每份套餐的售价应定为多少元时，既能保证利润又能吸引顾客？若不能，请说明理由．
答案解析收藏纠错 + 选题
9. 杭州休博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收33万元．而该游乐设施开放后，从第1个月到第x个月的维修保养费用累计为y（万元），且y=ax²+bx；若将创收扣除投资和维修保养费用称为游乐场的纯收益g（万元），g也是关于x的二次函数；
1. （1）若维修保养费用第1个月为2万元，第2个月为4万元．求y关于x的解析式；
2. （2）求纯收益g关于x的解析式；
3. （3）问设施开放几个月后，游乐场的纯收益达到最大；几个月后，能收回投资？
答案解析收藏纠错 + 选题
10. 有一种葡萄：从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的重量基本保持不变，现有一位个体户，按市场价收购了这种葡萄200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后每千克鲜葡萄的市场价格每天可以上涨0.2元，但是，存放一天需各种费用20元，平均每天还有1千克葡萄变质丢弃．
1. （1）设x天后每千克鲜葡萄的市场价为P元，写出P关于x的函数关系式;
2. （2）若存放x天后将鲜葡萄一次性出售，设鲜葡萄的销售金额为y元，写出y关于x的函数关系式；
3. （3）问个体户将这批葡萄存放多少天后出售，可获得最大利润，最大利润q是多少？
答案解析收藏纠错 + 选题
11. 绿色生态农场生产并销售某种有机产品，假设生产出的产品能全部售出．如图，线段EF、折线ABCD分别表示该有机产品每千克的销售价y₁（元）、生产成本y₂（元）与产量x（kg）之间的函数关系．
1. （1）求该产品销售价y₁（元）与产量x（kg）之间的函数关系式；
2. （2）直接写出生产成本y₂（元）与产量x（kg）之间的函数关系式；
3. （3）当产量为多少时，这种产品获得的利润最大？最大利润为多少？
答案解析收藏纠错 + 选题
12. 甲、乙两公司同时销售一款进价为40元/千克的产品．图①中折线ABC表示甲公司销售价y₁（元/千克）与销售量x（千克）之间的函数关系，图②中抛物线表示乙公司销售这款产品获得的利润y₂（元）与销售量x（千克）之间的函数关系．
1. （1）分别求出图①中线段AB、图②中抛物线所表示的函数表达式；
2. （2）当该产品销售量为多少千克时，甲、乙两公司获得的利润的差最大？最大值为多少？
答案解析收藏纠错 + 选题
13. 某公司销售某一种新型通讯产品，已知每件产品的进价为4万元，每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现，月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系
1. （1）求y关于x的函数关系式(直接写出结果)
2. （2）试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时，月获利最大?并求这个最大值
  (月获利一月销售额一月销售产品总进价一月总开支，)
3. （3）若公司希望该产品一个月的销售获利不低于5万元，借助(2)中函数的图象，请你帮助该公司确定销售单价的范围.在此情况下，要使产品销售量最大，你认为销售单价应定为多少万元
答案解析收藏纠错 + 选题
14. 某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，井建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P= $\text{[math]}$ （0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q= $\text{[math]}$
1. （1）当8＜t≤24时，求P关于t的函数解析式；
2. （2）设第t个月销售该原料药的月毛利润为w（单位：万元）
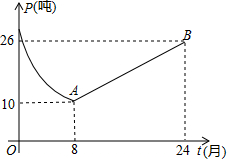
  ①求w关于t的函数解析式；
  ②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．
答案解析收藏纠错 + 选题
15. 每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送鲜花，感恩母亲，祝福母亲. 节日前夕，某花店采购了一批鲜花礼盒，成本价为30元每件，分析上一年母亲节的鲜花礼盒销售情况，得到了如下数据，同时发现每天的销售量 $\text{[math]}$ （件）是销售单价 $\text{[math]}$ （元/件）的一次函数.
销售单价 $\text{[math]}$ (元/件)
…
30
40
50
60
…
每天销售量 $\text{[math]}$ (件)
…
350
300
250
200
…
1. （1）求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系；
2. （2）物价局要求，销售该鲜花礼盒获得的利润不得高于100%：
  ①当销售单价 $\text{[math]}$ 取何值时，该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价)；
  ②试确定销售单价 $\text{[math]}$ 取何值时，花店销该鲜花礼盒每天获得的利润 $\text{[math]}$ （元）最大？并求出花店销该鲜花礼盒每天获得的最大利润.
答案解析收藏纠错 + 选题
16. 为了“创建文明城市，建设美丽家园”，我市某社区将辖区内的一块面积为1000m²的空地进行绿化，一部分种草，剩余部分栽花，设种草部分的面积为 $\text{[math]}$ （m²），种草所需费用 $\text{[math]}$ ₁（元）与 $\text{[math]}$ （m²）的函数关系式为 $\text{[math]}$ ，其图象如图所示：栽花所需费用 $\text{[math]}$ ₂（元）与x（m²）的函数关系式为 $\text{[math]}$ ₂=﹣0.01 $\text{[math]}$ ²﹣20 $\text{[math]}$ +30000（0≤ $\text{[math]}$ ≤1000）．
1. （1）请直接写出k₁、k₂和b的值；
2. （2）设这块1000m²空地的绿化总费用为W（元），请利用W与 $\text{[math]}$ 的函数关系式，求出绿化总费用W的最大值；
3. （3）若种草部分的面积不少于700m² ，栽花部分的面积不少于100m² ，请求出绿化总费用W的最小值．
答案解析收藏纠错 + 选题
17. 某经销商销售一种产品，这种产品的成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示：
1. （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
2. （2）求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时，每天的销售利润最大?最大利润是多少?
3. （3）该经销商想要每天获得168元的销售利润，销售价应定为多少?
答案解析收藏纠错 + 选题
18. 某批发部某一玩具价格如图所示，现有甲、乙两个商店，计划在“六一”儿童节前到该批发部购买此类玩具．两商店所需玩具总数为120个，乙商店所需数量不超过50个，设甲商店购买 $\text{[math]}$ 个．如果甲、乙两商店分别购买玩具，两商店需付款总和为y元．
1. （1）求y关于 $\text{[math]}$ 的函数关系式，并写出自变量 $\text{[math]}$ 的取值范围；
2. （2）若甲商店购买不超过100个，请说明甲、乙两商店联合购买比分别购买最多可节约多少钱；
3. （3） “六一”儿童节之后，该批发部对此玩具价格作了如下调整：数量不超过100个时，价格不变；数量超过100个时，每个玩具降价a元．在（2）的条件下，若甲、乙两商店“六一”儿童节之后去批发玩具，最多可节约2800元，求a的值．
答案解析收藏纠错 + 选题
19. 某电子厂商设计了一款制造成本为18元新型电子厂品，投放市场进行试销．经过调查，得到每月销售量y（万件）与销售单价x（元）之间的部分数据如下：
销售单价x（元/件）
…
20
25
30
35
…
每月销售量y（万件）
…
60
50
40
30
…
1. （1）求出每月销售量y（万件）与销售单价x（元）之间的函数关系式．
2. （2）求出每月的利润z（万元）与销售单x（元）之间的函数关系式．
3. （3）根据相关部门规定，这种电子产品的销售利润率不能高于50%，而且该电子厂制造出这种产品每月的制造成本不能超过900万元．那么并求出当销售单价定为多少元时，厂商每月能获得最大利润？最大利润是多少？（利润=售价﹣制造成本）
答案解析收藏纠错 + 选题
20. 天虹超市购进甲、乙两种水果，已知 1 千克甲种水果的进价比 1 千克乙种水果的进价多 4 元，购进 2千克甲种水果与 3 千克乙种水果共需 28 元.
1. （1）求甲种水果的进价为每千克多少元？
2. （2）经市场调查发现，甲种水果每天销售量 y(千克）与售价 m（元/千克）之间满足如图所示的函数关系，求 y与 m 之间的函数关系；
3. （3）在（2）的条件下，为减少库存，每天甲种水果的销售量不能低于 16 千克，当甲种水果的售价定为多少元时，才能使每天销售甲种水果的利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
21. 每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送鲜花，感恩母亲，祝福母亲. 节日前夕，某花店采购了一批鲜花礼盒，成本价为30元每件，分析上一年母亲节的鲜花礼盒销售情况，得到了如下数据，同时发现每天的销售量 $\text{[math]}$ （件）是销售单价 $\text{[math]}$ （元/件）的一次函数.
销售单价 (元/件)
…
30
40
50
60
…
每天销售量 $\text{[math]}$ (件)
…
350
300
250
200
…
1. （1）求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系；
2. （2）物价局要求，销售该鲜花礼盒获得的利润不得高于100%：
  ①当销售单价 $\text{[math]}$ 取何值时，该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价)；
  ②试确定销售单价 $\text{[math]}$ 取何值时，花店销该鲜花礼盒每天获得的利润 $\text{[math]}$ （元）最大？并求出花店销该鲜花礼盒每天获得的最大利润.
答案解析收藏纠错 + 选题
22. 大学毕业生小王响应国家“自主创业”的号召，利用银行小额无息贷款开办了一家饰品店．该店购进一种今年新上市的饰品进行销售，饰品的进价为每件40元，售价为每件60元，每月可卖出300件．市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件．为了获得更大的利润，现将饰品售价调整为60+x（元/件）（x＞0即售价上涨，x＜0即售价下降），每月饰品销量为y（件），月利润为w（元）．
1. （1）直接写出y与x之间的函数关系式；
2. （2）如何确定销售价格才能使月利润最大？求最大月利润；
3. （3）为了使每月利润不少于6000元应如何控制销售价格？
答案解析收藏纠错 + 选题
23. 2016年12月29日至31日，黔南州第十届旅游产业发展大会在“中国长寿之乡”﹣﹣罗甸县举行，从中寻找到商机的人不断涌现，促成了罗甸农民工返乡创业热潮．某“火龙果”经营户有A．B两种“火龙果”促销，若买2件A种“火龙果”和1件B种“火龙果”，共需120元；若买3件A种“火龙果”和2件B种“火龙果”，共需205元．
1. （1）设A，B两种“火龙果”每件售价分别为a元、b元，求a、b的值；
2. （2） B种“火龙果”每件的成本是40元，根据市场调查：若按（1）中求出的单价销售，该“火龙果”经营户每天销售B种“火龙果”100件；若销售单价每上涨1元，B种“火龙果”每天的销售量就减少5件．
  ①求每天B种“火龙果”的销售利润y（元）与销售单价x（元）之间的函数关系？
  ②求销售单价为多少元时，B种“火龙果”每天的销售利润最大，最大利润是多少？
答案解析收藏纠错 + 选题
24. 某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
1. （1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
2. （2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
答案解析收藏纠错 + 选题