浙江省宁波市余姚市兰江中学2022-2023学年九年级上学期...

更新时间：2024-07-29 浏览次数：83 类型：月考试卷

一、选择题（每小题4分，共40分，）

1. (2023九上·武汉期中) 抛物线y＝﹣（x﹣2）²+7的顶点坐标是（）

A . （﹣2，7） B . （﹣2，﹣7） C . （2，﹣7） D . （2，7）

答案解析收藏纠错 + 选题
2. (2022九上·余姚月考) 下列成语或词语所反映的事件中，发生的可能性大小最小的是（　　）

A . 守株待兔 B . 旭日东升 C . 瓜熟蒂落 D . 夕阳西下

答案解析收藏纠错 + 选题
3. (2022九上·余姚月考) 在70周年国庆阅兵式上有两辆阅兵车的车牌号如图所示（每辆阅兵车的车牌号含7位数字或字母），则“9”这个数字在这两辆车牌号中出现的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九上·余姚月考) 将y＝3x²通过平移，先向上平移2个单位，再向左平移3个单位，可得到抛物线是（）

A . y＝3（x+3）²﹣2 B . y＝3（x+3）²+2 C . y＝3（x+2）²﹣3 D . y＝3（x﹣2）²+3

答案解析收藏纠错 + 选题
5. (2022九上·余姚月考) 甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（　　）

A . 掷一枚正六面体的骰子，出现1点的概率 B . 一个袋子中有2个白球和1个红球，从中任取一个球，则取到红球的概率 C . 抛一枚硬币，出现正面的概率 D . 任意写一个整数，它能被2整除的概率

答案解析收藏纠错 + 选题
6. (2022九上·余姚月考) 二次函数 $\text{[math]}$ 的图象（1≤x≤3）如图所示，则该函数在所给自变量的取值范围内，函数值y的取值范围是（）

A . y≥1 B . 1≤y≤3 C . $\text{[math]}$ D . 0≤y≤3

答案解析收藏纠错 + 选题
7. (2022九上·余姚月考) 在﹣2，﹣1，0，1，2这五个数中任取两数m，n，则二次函数y=（x﹣m）²+n的顶点在坐标轴上的概率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·余姚月考) 若点A（﹣1，y₁），B（2，y₂），C（3，y₃）在抛物线y＝﹣2x²+8x+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（　　）

A . y₃＜y₂＜y₁ B . y₂＜y₁＜y₃ C . y₁＜y₃＜y₂ D . y₃＜y₁＜y₂

答案解析收藏纠错 + 选题
9. (2022九上·余姚月考) 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是抛物线y＝ax²﹣2ax上的点．下列命题：①若a＞0，且|x₁﹣1|＞|x₂﹣1|，则y₁＞y₂；②若a＜0，且|x₁﹣1|＞|x₂﹣1|，则y₁＜y₂；③若|x₁﹣1|＝|x₂﹣1|，则y₁＝y₂；④若y₁＝y₂ ，则x₁＝x₂ ，正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2022九上·余姚月考) 已知抛物线y＝ax²+bx+c与x轴交于点A（﹣1，0），与y轴的交点在（0，2），（0，3）之间（包含端点），顶点坐标为（1，n），则下列结论正确的有（）
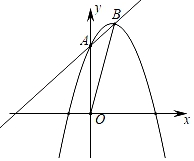
①2a+b＜0；②﹣1≤a≤﹣ $\text{[math]}$ ；③对于任意实数m，a（m²﹣1）+b（m﹣1）≤0总成立；④关于x的方程ax²+bx+c＝n+1有两个不相等的实数根．

A . ①③④ B . ②③ C . ② D . ②③④

答案解析收藏纠错 + 选题

二、填空题（每小题5分，共30分）

11. (2022九上·余姚月考) 抛物线y＝x²+2x+2与y轴交点坐标为．

答案解析收藏纠错 + 选题
12. (2022九上·余姚月考) “一只不透明的袋子共装有3个小球，它们的标号分别为1，2，3，从中摸出1个小球，标号为“4”，这个事件是．（填“必然事件”、“不可能事件”或“随机事件”）

答案解析收藏纠错 + 选题
13. (2024九上·驻马店期末) 在一个不透明的布袋中装有52个白球和若干个黑球，除颜色外其他都相同，小强每次摸出一个球记录下颜色后并放回，通过多次试验后发现，摸到黑球的频率稳定在0.2左右，则布袋中黑球的个数可能有．

答案解析收藏纠错 + 选题
14. (2022九上·余姚月考) 王翔同学在一次跳高训练中采用了背跃式，跳跃路线正好和抛物线y＝﹣2x²+3x+ $\text{[math]}$ 相吻合，那么他能跳过的最大高度为m．

答案解析收藏纠错 + 选题

15. (2022九上·余姚月考) 已知二次函数自变量的部分的取值和对应的函数值如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	5	0	﹣3	﹣4	﹣3	0	…

则在实数范围内能使得y﹣5＞0成立的取值范围是．

答案解析收藏纠错 + 选题

16. (2022九上·余姚月考) 在平面直角坐标系中，点C、B分别在x轴、y轴上，△ABC是等腰直角三角形，∠BAC＝90°，已知A（2，2）、P（1，0）．M为BC的中点，当PM最短时，则M的坐标为．

答案解析收藏纠错 + 选题

三、解答题（第17～19题各8分，第20-22题各10分，第23题12分，第24题14分，共80分）

17. (2022九上·余姚月考) 已知抛物线y＝﹣x²+bx﹣c的部分图象如图．
1. （1）求b、c的值；
2. （2）分别求出抛物线的对称轴和y的最大值．
答案解析收藏纠错 + 选题

18. (2022九上·余姚月考) 在一个不透明的袋子中装有红、黄两种颜色的球共20个，每个球除颜色外完全相同．某学习兴趣小组做摸球试验，将球搅匀后从中随机摸出1个球，记下颜色后再放回袋中，不断重复．下表是活动进行中的部分统计数据．

摸球的次数n	100	150	200	500	800	1000
摸到红球的次数m	59	96	118	290	480	600
摸到红球的频率 $\text{[math]}$	0.59		0.58		0.60	0.60

（1）完成上表；
（2） “摸到红球”的概率的估计值．（精确到0.1）
（3）试估算袋子中红球的个数．

答案解析收藏纠错 + 选题

19. (2022九上·余姚月考) 已知二次函数y＝﹣x²+mx+m﹣2的顶点为A，且经过点（2，0）．
1. （1）求顶点A的坐标；
2. （2）把该二次函数以y轴为对称轴作轴对称变换，求变化后的函数表达式．
答案解析收藏纠错 + 选题
20. (2022九上·余姚月考) 余姚全面推进生活垃圾分类工作，如图是某小区放置的垃圾桶，从左到右依次是绿色：厨余垃圾；蓝色：可回收垃圾；黑色：其他垃圾；红色：有害垃圾．
1. （1）居民A将一袋厨余垃圾随手放入一个垃圾桶，他能正确投放垃圾的概率是．
2. （2）居民B手拎两袋垃圾，一袋是可回收垃圾，另一袋是有害垃圾，她先将可回收垃圾随手放入一个垃圾桶，然后把另一袋垃圾又随手放入另外的垃圾桶中的一个．问：两袋垃圾都投放正确的概率？请画出树状图或列表说明理由．
答案解析收藏纠错 + 选题
21. (2022九上·余姚月考) 如图，直线y＝x+m与二次函数y＝ax²+2x+c的图象交于点A（0，3），已知该二次函数图象的对称轴为直线x＝1.
1. （1）求m的值及二次函数解析式；
2. （2）若直线y＝x+m与二次函数y＝ax²+2x+c的图象的另一个交点为B，求△OAB的面积；
3. （3）根据函数图象回答：x为何值时该一次函数值大于二次函数值.
答案解析收藏纠错 + 选题
22. (2022九上·余姚月考) 已知二次函数y＝x²﹣2mx+2m﹣1（m为常数）．
1. （1）求证：不论m为何值，该二次函数的图象与x轴总有公共点．
2. （2）求证：不论m为何值，该二次函数的图象的顶点都在函数y＝﹣（x﹣1）²的图象上．
3. （3）已知点A（a，﹣1）、B（a+2，﹣1），线段AB与函数y＝﹣（x﹣1）²的图象有公共点，则a的取值范围是．
答案解析收藏纠错 + 选题
23. (2022九上·余姚月考) 某商店销售一种纪念册，每本进价 $\text{[math]}$ 元，规定销售单价不低于 $\text{[math]}$ 元，且获利不高于 $\text{[math]}$ 在销售期间发现销售数量 $\text{[math]}$ （件）与销售单价 $\text{[math]}$ （元）的关系如下表：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
1. （1）请你根据表格直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出自变量 $\text{[math]}$ 的取值范围；
2. （2）当每本纪念册销售单价是多少元时，商店每天获利 $\text{[math]}$ 元?
3. （3）将这种纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润 $\text{[math]}$ （元）最大?最大利润是多少元?
答案解析收藏纠错 + 选题
24. (2022九上·余姚月考) 定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”，如图①，抛物线C₁：y＝x²+2x﹣3与抛物线C₂：y＝ax²+2ax+c组成一个开口向上的“月牙线”，抛物线C₁和抛物线C₂与x轴有着相同的交点A（﹣3，0）、B（点B在点A右侧），与y轴的交点分别为G、H（0，﹣1）．
1. （1）求抛物线C₂的解析式和点G的坐标．
2. （2）点M是x轴下方抛物线C₁上的点，过点M作MN⊥x轴于点N，交抛物线C₂于点D，求线段MN与线段DM的长度的比值．
3. （3）如图②，点E是点H关于抛物线对称轴的对称点，连接EG，在x轴上是否存在点F，使得△EFG是以EG为腰的等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省宁波市余姚市兰江中学2022-2023学年九年级上学期...

副标题：

*注意事项：

浙江省宁波市余姚市兰江中学2022-2023学年九年级上学期...

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$