 B .
B .  C .
C .  D .
D . 



常用的分解因式的方法有提取公因式法、公式法等,但有的多项式则不能直接用上述两种方法进行分解,比如多项式. . 这样我们就需要结合式子特点,探究新的分解方法.仔细观察这个四项式,会发现:若把它的前两项结合为一组符合平方差公式特点,把它的后两项结合为一组可提取公因式,而且对前后两组分别进行因式分解后会出现新的公因式,提取新的公因式就可以完成对整个式子的因式分解.具体过程如下:
例1:
……………………分成两组
………………分别分解
………………………提取公因式完成分解
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.分组分解法一般是针对四项或四项以上的多项式,关键在恰当分组,分组须有“预见性”,预见下一步能继续分解,直到完成分解.
;
.
课外兴趣小组活动时,老师提出了如下问题:

如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
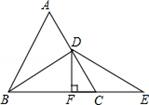
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.