浙江省温州市2022-2023学年九年级上学期第一次月考数学...

更新时间：2024-07-13 浏览次数：89 类型：月考试卷

一、单选题

1. (2022九上·温州月考) 有10张背面完全相同的卡片，正面分别写有数字：1至10，把这些卡片背面朝上洗匀后，从中随机抽取三张卡片a，b，c，则这三张卡片a，b，c的数字正好是直角三角形的三边长的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·温州月考) 已知⊙O的半径为13，弦AB∥CD，AB=24，CD=10，则四边形ACDB的面积是（）

A . 119 B . 289 C . 77或119 D . 119或289

答案解析收藏纠错 + 选题
3. (2022九上·温州月考) 如图， $\text{[math]}$ 是由等腰直角 $\text{[math]}$ 经过位似变换得到的，位似中心在 $\text{[math]}$ 轴的正半轴，已知 $\text{[math]}$ ， $\text{[math]}$ 点坐标为 $\text{[math]}$ ，位似比为 $\text{[math]}$ ，则两个三角形的位似中心 $\text{[math]}$ 点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·黄陂自主招生) 定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ ，点 $\text{[math]}$ ，则互异二次函数 $\text{[math]}$ 与正方形 $\text{[math]}$ 有交点时 $\text{[math]}$ 的最大值和最小值分别是（）

A . 4，-1 B . $\text{[math]}$ ，-1 C . 4，0 D . $\text{[math]}$ ，-1

答案解析收藏纠错 + 选题
5. (2022九上·莒南期中) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别在AC和BC上， $\text{[math]}$ ，若以DE为直径的⊙O交AB的中点F，则⊙O的直径是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
6. (2022九上·温州月考) 如图，△ABC为等腰直角三角形，∠BAC＝90°，AB＝AC＝2，点D为△ABC所在平面内一点，∠BDC＝90°，以AC、CD为边作平行四边形ACDE，则CE的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九上·温州月考) 如图1，是清代数学家李之铉在他的著作《几何易简集》中研究过的一个图形，小圆同学在研究该图形后设计了图2，延长正方形 $\text{[math]}$ 的边 $\text{[math]}$ 至点 $\text{[math]}$ ，作矩形 $\text{[math]}$ ，以 $\text{[math]}$ 为直径作半圆 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边做正方形 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 上，记正方形 $\text{[math]}$ ，正方形 $\text{[math]}$ ，矩形 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·温州月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，将矩形沿 $\text{[math]}$ 翻折，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边 $\text{[math]}$ 处，连接 $\text{[math]}$ ，在 $\text{[math]}$ 上取点 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作⊙O与 $\text{[math]}$ 相切于点 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论：① $\text{[math]}$ 是 $\text{[math]}$ 的中点；②⊙O的半径是2；③ $\text{[math]}$ ；④S_阴影 $\text{[math]}$ .其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2022九上·温州月考) 如图，抛物线 $\text{[math]}$ 交x轴于A，B两点，交y轴于点C，点D为抛物线的顶点，点C关于抛物线的对称轴的对称点为点E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·温州月考) 如图，边长为6的正方形ABCD中，E、F是对角线AC的三等分点，连接BE并延长交AD于点G，连接GF并延长交BC于点H，记△GEF的面积为m，△CHF的面积为n，则m+n的值为（）

A . $\text{[math]}$ B . 6 C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·沭阳期中) 若实数a是一元二次方程x²-3x+1=0的一个根，则a³+ $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
12. (2022九上·温州月考) 温故知新：若满足不等式 $\text{[math]}$ 的整数k只有一个，则正整数n的最大值．
阅读理解：任意正整数 $\text{[math]}$ ， $\text{[math]}$ ， ∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ， ∴ $\text{[math]}$ ，只有当 $\text{[math]}$ 时，等号成立；结论：在 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 均为正实数）中，只有当 $\text{[math]}$ 时， $\text{[math]}$ 有最小值 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ 有最小值为．

答案解析收藏纠错 + 选题
13. (2022九上·温州月考) 如图是一个小圆同学设计的一个鱼缸截面图，弓形 $\text{[math]}$ 是由优弧 $\text{[math]}$ 与弦 $\text{[math]}$ 组成， $\text{[math]}$ 是鱼缸的玻璃隔断，弓形 $\text{[math]}$ 部分不注水，已知 $\text{[math]}$ ，且圆心 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ．注水时，当水面恰好经过圆心时，则水面宽 $\text{[math]}$ 为 $\text{[math]}$ ；注水过程中，求水面宽度 $\text{[math]}$ 的最大值为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2022九上·温州月考) 已知抛物线y₁：y＝2（x﹣3）²+1和抛物线y₂：y＝﹣2x²﹣8x﹣3，若无论k取何值，直线y＝kx+km+n被两条抛物线所截的两条线段都保持相等，则m＝，n＝．

答案解析收藏纠错 + 选题
15. (2022九上·温州月考) 工人师傅在修茸一人字架屋顶BAC时需要加固，计划焊接三根钢条AD，DE，FG．在如图所示的△ABC中，AB=AC=10，BC=12，AD⊥BC于点D，点E，F，G分别是AB，BD，AC上的点，连接DE，GF，交于点H，GF与AD交于点M，当H为FM的中点，BF∶CF=1∶5，AG：AE=5：7时，△AGM的面积为．

答案解析收藏纠错 + 选题
16. (2022九上·温州月考) 图甲是一款设计师工作台灯，它的主要构件是上下两条旋转臂和一盏条形灯.设计师工作时，常常通过转动旋转臂和灯来调节光源的位置，获得需要的光照效果图乙表示了设计师两次调节过程，他先转动下旋转臂 $\text{[math]}$ ，使点 $\text{[math]}$ 到桌面的距高 $\text{[math]}$ ，然后转动上旋转臂 $\text{[math]}$ 和灯 $\text{[math]}$ ，使 $\text{[math]}$ 与桌面 $\text{[math]}$ 平行，且 $\text{[math]}$ .调好后他感觉光照效果不佳，于是再转动上旋转臂和灯，使得上旋转臂 $\text{[math]}$ ，同时灯 $\text{[math]}$ .若已知上旋转臂 $\text{[math]}$ ，第二次调整后灯向右移动的水平距离 $\text{[math]}$ ，则第二次调整结束后灯距高桌面的高度 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

17. (2022九上·温州月考) 如图，已知二次函数G₁：y＝ax²+bx+c（a≠0）的图象过点（﹣1，0）和（0，3），对称轴为直线x＝1．
1. （1）求二次函数G₁的解析式；
2. （2）当﹣1＜x＜2时，求函数G₁中y的取值范围；
3. （3）将G₁先向右平移3个单位，再向下平移2个单位，得到新二次函数G₂ ，则函数G₂的解析式是．
4. （4）当直线y＝n与G₁、G₂的图象共有4个公共点时，直接写出n的取值范围．
答案解析收藏纠错 + 选题
18. (2022九上·温州月考) 已知圆O的半径长为2，点A、B、C为圆O上三点，弦 $\text{[math]}$ ，点D为BC的中点，
1. （1）如图，连接AC、OD，设 $\text{[math]}$ ，请用α表示 $\text{[math]}$ ；
2. （2）如图，当点B为 $\text{[math]}$ 的中点时，求点A、D之间的距离．
3. （3）如果AD的延长线与圆O交于点E，以O为圆心，AD为半径的圆与以BC为直径的圆有且只有一个交点，求弦AE的长．
答案解析收藏纠错 + 选题
19. (2022九上·温州月考) 已知如图，E、F分别在四边形ABCD边AB、BC上，在CD上求作一点P，使 $\text{[math]}$ ．（不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题
20. (2022九上·温州月考) 阅读材料：各类方程的解法：求解一元一次方程，根据等式的基本性质，把方程转化为 $\text{[math]}$ 的形式，求解二元一次方程组，把它转化为一元一次方程来解；类似的，三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想——转化，把未知转化为已知．
1. （1）问题：方程 $\text{[math]}$ 的解是： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）拓展：用“转化”思想求方程 $\text{[math]}$ 的解；
3. （3）应用：如图，矩形草坪 $\text{[math]}$ 的长 $\text{[math]}$ ，宽 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上（ $\text{[math]}$ ），小华把一根长为27m的绳子一段固定在点 $\text{[math]}$ ，把长绳 $\text{[math]}$ 段拉直并固定在点 $\text{[math]}$ ，再拉直，长绳的另一端恰好落在点 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
21. (2022九上·温州月考)
1. （1）把长为 $\text{[math]}$ 的线段任意分成3条线段，求这3条线段能够构成一个三角形的3条边的概率．
2. （2）据统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．为了保护环境，缓解汽车拥堵，该市拟控制汽车总量，要求到2012年底全市汽车拥有量不超过125.48万辆；且从2011年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的 $\text{[math]}$ ．假设每年新增汽车数量相同，请估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆，并求出求2008年底至2010年底该市汽车拥有量的年平均增长率．
答案解析收藏纠错 + 选题
22. (2022九上·温州月考) 在平面直角坐标系中，二次函数 $\text{[math]}$ （ $\text{[math]}$ ， m为常数）的图象记作G，图象G上点A的横坐标为2m．
1. （1）当 $\text{[math]}$ ，求图象G的最低点坐标；
2. （2）平面内有点 $\text{[math]}$ ．当AC不与坐标轴平行时，以AC为对角线构造矩形ABCD，AB与x轴平行，BC与y轴平行．
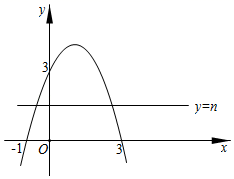
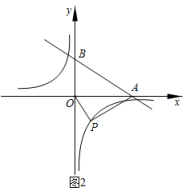
  ①若矩形ABCD为正方形时，求点A坐标；
  ②图象G与矩形ABCD的边有两个公共点时，求m的取值范围．
答案解析收藏纠错 + 选题

23. (2022九上·温州月考) 某工厂每月生产800件产品，每件产品成本100元，分配给线下直营店和线上旗舰店两个渠道销售．线下直营店的产品按照定价190元出售，并进行促销活动：月销量不超过400件的部分，每件产品赠送成本为60元的礼品，可全部售完；超过400 件的部分，因礼品已送完，则需要再一次性投入成本为5000元的广告进行宣传，也可全部售完．线上旗舰店的产品售价 $\text{[math]}$ （元）与月销量 $\text{[math]}$ （件）满足关系： $\text{[math]}$ ．（销售利润 $\text{[math]}$ 销售收入-成本）

（1）分别用含 $\text{[math]}$ 的代数式表示：
①线下直营店的月销量为 $\text{[math]}$ 件．若 $\text{[math]}$ 这 $\text{[math]}$ 件产品的销售利润为元；若 $\text{[math]}$ 这 $\text{[math]}$ 件产品的销售利润为元．

②线上旗舰店的月销量为 $\text{[math]}$ 件，这 $\text{[math]}$ 件产品的销售利润为元．

（2）假设800件产品每月都能售出．

①若平均分配给两个渠道进行销售，求这800件产品的销售总利润．

②请设计一种与①不同的分配方案，根据方案评价表，确定方案类型并填表．（不同方案得分不同，具体见表）

线下直营店分配数量		线上旗舰店分配数量	你的方案类型（填优秀、良好或合格）
件		件
方案评价表（利润单位：元）
优秀方案	月总利润 $\text{[math]}$	4 分
良好方案	$\text{[math]}$ 月总利润 $\text{[math]}$	2 分
合格方案	$\text{[math]}$ 月总利润 $\text{[math]}$	1 分

答案解析收藏纠错 + 选题

24. (2022九上·温州月考) 四边形的一条对角线将这个四边形分成两个三角形，如果这两个三角形相似（不全等），那么我们将这条对角线叫做这个四边形的相似对角线．
1. （1）如图1，四边形ABCD中，∠DAB＝100°，∠DCB＝130°，对角线AC平分∠DAB，求证：AC是四边形ABCD的相似对角线；
2. （2）如图2，直线 $\text{[math]}$ 分别与x，y轴相交于A，B两点，P为反比例函数y＝ $\text{[math]}$ （k＜0）上的点，若AO是四边形ABOP的相似对角线，求反比例函数的解析式；
3. （3）如图3，AC是四边形ABCD的相似对角线，点C的坐标为（3，1），AC∥x轴，∠BCA＝∠DCA＝30°，连接BD，△BCD的面积为 $\text{[math]}$ ．过A，C两点的抛物线y＝ax²+bx+c（a＜0）与x轴交于E，F两点，记|m|＝AC+1，若直线y＝mx与抛物线恰好有3个交点，求实数a的值．
答案解析收藏纠错 + 选题