22.
(2022高二上·郑州期末)
在水平桌面上放一只内壁光滑的玻璃水杯,已知水杯内壁为抛物面型(抛物面指抛物线绕其对称轴旋转

所得到的面),抛物面的轴截面是如图所示的抛物线.现有一些长短不一、质地均匀的细直金属棒,其长度均不小于抛物线通径的长度(通径是过抛物线焦点,且与抛物线的对称轴垂直的直线被抛物线截得的弦),若将这些细直金属棒,随意丢入该水杯中,实验发现:当细棒重心最低时,达到静止状态,此时细棒交汇于一点.
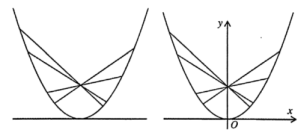

,
, 命题
__________,若
是
的充分不必要条件,求实数
的取值范围.
