22.
(2022·攀枝花)
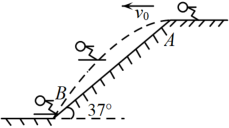
第24届冬奥会(也称2022年北京冬奥会)于2022年2月4日至2月20日在中国北京举行,北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆,整个动作连贯一致,一气呵成,如图,某运动员穿着滑雪板,经过助滑后,从倾斜角

的跳台A点以速度

沿水平方向跳出,若忽略空气阻力影响,水平方向速度将保持不变.同时,由于受重力作用,运动员沿竖直方向会加速下落,因此,运动员在空中飞行的路线是抛物线的一部分,已知该运动员在B点着陆,

, 且

.忽略空气阻力,请回答下列问题:
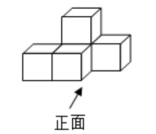
 B .
B .  C .
C .  D .
D . 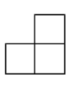
![]()

是平行四边形;
时,四边形
是矩形;
时,四边形
是菱形;
, 且
时,四边形
是正方形.