江苏省扬州市高邮市2021-2022学年七年级上学期期末数学...

更新时间：2024-07-13 浏览次数：138 类型：期末考试

一、单选题

1. (2022七上·高邮期末) 当前手机移动支付已经成为新型的支付方式，图中是妈妈元旦当天的微信零钱支付明细，则妈妈元旦当天的微信零钱收支情况是（）
转账-来自SNM
+48
云视听极光
-30
扫二维码付款
-50

A . 收入128元 B . 收入32元 C . 支出128元 D . 支出32元

答案解析收藏纠错 + 选题
2. (2022七上·高邮期末) 无理数 $\text{[math]}$ 在数轴上位置的描述，正确的是（）

A . 在点-4的左边 B . 在点-3的右边 C . 和原点的距离小于3 D . 和原点的距离大于3

答案解析收藏纠错 + 选题
3. (2023七上·仪征月考) 在有理数﹣3² ， 3.5，﹣（﹣3），|﹣2|、（﹣ $\text{[math]}$ ）² ， ﹣3.1415926中，负数的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
4. (2022七上·高邮期末) 如图，把一个圆剪去一部分，所得涂色部分的图形周长比原来圆的周长小，能正确解释这一现象的数学知识是（）

A . 垂线段最短 B . 两点确定一条直线 C . 两点之间，线段最短 D . 经过一点有无数条直线

答案解析收藏纠错 + 选题
5. (2022七上·高邮期末) 若钝角∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系满足（）

A . ∠1-∠3＝90° B . ∠1+∠3＝90° C . ∠1+∠3＝180° D . ∠1＝∠3

答案解析收藏纠错 + 选题
6. (2022七上·高邮期末) 我国古代的数学专著《九章算术》中有这样一道题：“今有人共买物，人出七，盈二；人出六，不足四，问人数，物价各几何？”译文：“几个人一起去购买某物品，若每人出7钱，则多了2钱；若每人出6钱，则少了4钱，问有多少人，物品的价格是多少？”设有x人，可列方程为（）

A . 7x-2＝6x+4 B . 7x+2＝6x+4 C . 7x-2＝6x-4 D . 7x+2＝6x-4

答案解析收藏纠错 + 选题
7. (2023七上·仪征月考) 已知点M在线段AB上，点N是线段MB的中点，若AN＝6，则AM+AB的值为（）

A . 10 B . 8 C . 12 D . 以上答案都不对

答案解析收藏纠错 + 选题
8. (2022七上·高邮期末) 如图，在这个数运算程序中，若开始输入的正整数n为奇数，都计算3n+1；若n为偶数，都除以2.若n＝21时，经过1次上述运算输出的数是64；经过2次上述运算输出的数是32；经过3次上述运算输出的数是16；…；经过2022次上述运算输出的数是（）.

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

9. (2023七上·仪征月考) 天宫二号是中国首个具备补加功能的载人航天科学实验空间实验室，天宫二号的轨道高度约为393000m，393000m用科学记数法表示为 m.

答案解析收藏纠错 + 选题
10. (2023七上·仪征月考) 在下列各数中：2022， $\text{[math]}$ ， $\text{[math]}$ ， 3.1010010001…（每两个1之间的0依次加1），无理数有个.

答案解析收藏纠错 + 选题
11. (2022七上·高邮期末) 若关于x、y的单项式x^a+7y⁵与-2x³y^3b-¹的和仍是单项式，则ab的值是.

答案解析收藏纠错 + 选题
12. (2023七上·仪征月考) 爱动脑筋的小明学习《实验手册》钟面上的数学问题时，计算出晚上放学时间8时30分，钟面上时针和分针的夹角为 °.

答案解析收藏纠错 + 选题
13. (2022七上·高邮期末) 如图，把该正方体展开图折叠成正方体后，“邮”字对面的字是.

答案解析收藏纠错 + 选题
14. (2022七上·高邮期末) 若方程（m+1）x^2|m^|^-¹+2＝0是关于x的一元一次方程，则m的值是 .

答案解析收藏纠错 + 选题
15. (2023七上·仪征月考) M、N是数轴上的两个点，线段MN的长度为4，若点M表示的数为 $\text{[math]}$ ，则点N表示的数为．

答案解析收藏纠错 + 选题
16. (2022七上·高邮期末) 已知代数式x+2y的值是-2，则1-2x-4y的值是 .

答案解析收藏纠错 + 选题
17. (2022七上·高邮期末) 一个长方体包装盒展开后如图所示（单位：cm），则其容积为 cm³.

答案解析收藏纠错 + 选题
18. (2022七上·高邮期末) 我们知道，一个数a的绝对值|a|即数轴上表示这个数的点到原点的距离，而|a|可以写成|a-0|，推广到一般情况就是，若两个数a、b分别对应数轴上两个点A、B，则|a-b|即A、B两点之间的距离.若x对应数轴上任意一点P，则|x+3|-|x-5|的最大值是 .

答案解析收藏纠错 + 选题

三、解答题

19. (2022七上·高邮期末) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2022七上·高邮期末) 解方程
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2022七上·高邮期末) 先化简，再求值：3（x²y+xy）-2（x²y-xy）-4x²y-3，其中x、y满足|x+1|+（y-1）²＝0.

答案解析收藏纠错 + 选题
22. (2022七上·高邮期末) 如图，A、B、C为网格图中的三点，利用网格作图.
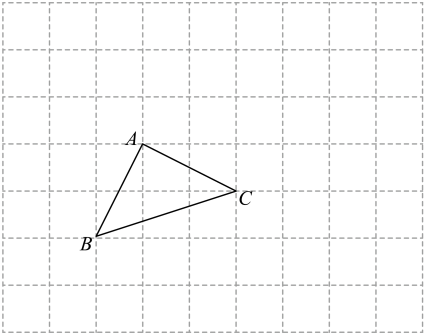
⑴过点A画直线AD∥BC；
⑵过点A画线段BC的垂线AH，垂足为H；
⑶点A到直线BC的距离是线段 ▲ 的长；
⑷三角形ABC的面积为 ▲ .

答案解析收藏纠错 + 选题
23. (2022七上·高邮期末) 补全下面的解题过程：
如图，已知OC是∠AOB内部的一条射线，OD是∠AOB的平分线，∠AOC＝2∠BOC，且∠BOC＝40°，求∠COD的度数.
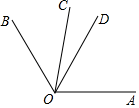
解：∵∠AOC＝2∠BOC，∠BOC＝40°，
∴∠AOC＝      ▲      °.
∴∠AOB＝∠AOC+∠      ▲      ＝      ▲      °.
∵OD平分∠AOB，
∴∠AOD＝ $\text{[math]}$ ∠AOB＝      ▲      °.
∴∠COD＝∠      ▲      -∠AOD＝20°.

答案解析收藏纠错 + 选题
24. (2022七上·高邮期末) 如图，用若干个棱长为1cm的小正方体搭成一个几何体.
1. （1）分别画出这个几何体的三视图；
2. （2）若将这个几何体外表面涂上一层漆，则其涂漆面积为cm²；
3. （3）现添加若干个上述小正方体后，若保持左视图和俯视图不变，最多还可以再添加块小正方体.
答案解析收藏纠错 + 选题
25. (2022七上·高邮期末) 接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每人每小时生产疫苗500剂，但受某些因素影响，某车间有10名工人不能按时到厂.为了应对疫情，该车间其余工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天能完成预定任务.
1. （1）求该车间当前参加生产的工人有多少人；
2. （2）生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时.若上级分配给该车间共780万剂的生产任务，问该车间还需要多少天才能完成任务.
答案解析收藏纠错 + 选题
26. (2022七上·高邮期末) 已知关于x的一元一次方程ax+b＝0（其中a≠0，a、b为常数），若这个方程的解恰好为x＝a-b，则称这个方程为“恰解方程”，例如：方程2x+4＝0的解为x＝-2，恰好为x＝2-4，则方程2x+4＝0为“恰解方程”.
1. （1）已知关于x的一元一次方程3x+k＝0是“恰解方程”，则k的值为；
2. （2）已知关于x的一元一次方程-2x＝mn+n是“恰解方程”，且解为x＝n（n≠0）.求m，n的值；
3. （3）已知关于x的一元一次方程3x＝mn+n是“恰解方程”.求代数式3（mn+2m²-n）-（6m²+mn）+5n的值.
答案解析收藏纠错 + 选题
27. (2022七上·高邮期末) 如图1，已知射线OB在∠AOC内，若满足∠BOC+∠AOC＝180°，则称射线OB为∠BOC与∠AOC的“互补线”.
1. （1）如图2，已知点O是直线AD上一点，射线OB、OC在直线AD同侧，且射线OC平分∠BOD.试说明：射线OB为∠BOC与∠AOC的“互补线”；
2. （2）如图3，已知直线AB、CD相交于点O，射线OE为∠BOC与∠BOE的“互补线”，若∠AOD＝136°，求∠DOE的度数；
3. （3）如图4，已知射线OB为∠BOC与∠AOC的“互补线”，且射线OE、OF分别平分∠AOC、∠BOC，试判断∠BOC+∠EOF的度数是否为定值，若为定值，求出定值的度数；若不为定值，请说明理由.
答案解析收藏纠错 + 选题
28. (2022七上·高邮期末) 如图1，已知线段AE＝48Cm，点B、C、D在线段AD上，且AB：BC：CD：DE＝1：2：1：2.
1. （1） BC＝cm，CD＝cm；
2. （2）已知动点M从点A出发，以2cm/s的速度沿A-B-C-D-E向点E运动；同时动点N从点E出发，以1cm/s的速度沿E-D-C-B-A向点A运动，当点M到达点E后立即以原速返回，直到点N到达点A，运动停止；设运动的时间为t.
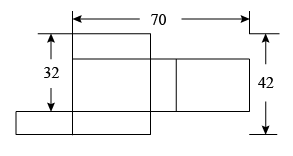
  ①求t为何值，线段MN的长为12cm；
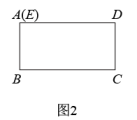
  ②如图2，现将线段AE折成一个长方形ABCD（点A、E重合），请问：是否存在某一时刻，以点A、B、M、N为顶点的四边形面积与以点C、D、M、N为顶点的四边形面积相等，若存在，求出t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题