山西省临汾市2022-2023学年九年级上学期期中数学试卷

更新时间：2023-01-29 浏览次数：55 类型：期中考试

一、单选题

1. (2022九上·临汾期中) 计算 $\text{[math]}$ 的结果为（）

A . 2 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·衡南期中) 下列各组中的四条线段成比例的是（）

A . 4、2、1、3 B . 1、2、3、5 C . 3、4、5、6 D . 1、2、2、4

答案解析收藏纠错 + 选题
3. (2022九上·临汾期中) 我们在解一元二次方程 $\text{[math]}$ 时，先将等号左边利用平方差公式进行因式分解，得到 $\text{[math]}$ ，再把它转化为两个一元一次方程 $\text{[math]}$ 或 $\text{[math]}$ ，进而解得 $\text{[math]}$ ， $\text{[math]}$ ，这种解方程的过程体现出来的数学思想是（　　）

A . 抽象的思想 B . 数形结合的思想 C . 公理化的思想 D . 转化的思想

答案解析收藏纠错 + 选题
4. (2022九上·临汾期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ （　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·新蔡期中) 下列计算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九上·临汾期中) 图1是伸缩折叠不锈钢晾衣架的实物图，图2是它的侧面示意图， $\text{[math]}$ 和 $\text{[math]}$ 相交于点O，点A，B之间的距离为1.2米， $\text{[math]}$ ，根据图2中的数据可得点C，D之间的距离为（　　）

A . 0.8米 B . 0.86米 C . 0.96米 D . 1米

答案解析收藏纠错 + 选题
7. (2022九上·临汾期中) 用配方法解方程 $\text{[math]}$ ，配方后所得的方程是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·临汾期中) 如图，E是 $\text{[math]}$ 的边 $\text{[math]}$ 的延长线上的一点，连接 $\text{[math]}$ ，交边 $\text{[math]}$ 于点P．若 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·汝南模拟) 关于一元二次方程 $\text{[math]}$ （k为常数）的根的情况，下列说法正确的是（　　）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 不能确定根的情况

答案解析收藏纠错 + 选题
10. (2022九上·临汾期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， E，F分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P为边 $\text{[math]}$ 上一点，过点P作 $\text{[math]}$ ，交 $\text{[math]}$ 于点Q，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（　　）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·临汾期中) $\text{[math]}$ 化为最简二次根式是．

答案解析收藏纠错 + 选题
12. (2022九上·临汾期中) 蝴蝶标本可以近似地看作轴对称图形．如图，将一只蝴蝶标本放在平面直角坐标系中，如果图中点A的坐标为（5，3），则其关于y轴对称的点B的坐标为．

答案解析收藏纠错 + 选题
13. (2023·宁江模拟) 如图，在 $\text{[math]}$ 中，D是 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ，垂足为E，F是 $\text{[math]}$ 的中点， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. (2022九上·临汾期中) 如图，在某小区内拐角处的一段道路上，有一儿童在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点O），已知 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，则汽车从A处前行的距离 $\text{[math]}$ 米时，才能发现C处的儿童．

答案解析收藏纠错 + 选题
15. (2022九上·临汾期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2022九上·临汾期中)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2022九上·临汾期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， E是边AC上一点，且 $\text{[math]}$ ，过点A作BE的垂线，交BE的延长线于点D，求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023九上·沭阳期中) 某超市以每箱25元的进价购进一批水果，当该水果售价为40元/箱时，六月销售256箱，七、八月该水果十分畅销，销量持续上涨，在售价不变的基础上，八月的销量达到400箱．
1. （1）求七，八两月的月平均增长率；
2. （2）九月该超市为了减少库存，开始降价促销，经调查发现，该水果每箱降价1元，月销量在八月销量的基础上增加5箱，当该水果每箱降价多少元时，超市九月获利4250元？
答案解析收藏纠错 + 选题
19. (2022九上·临汾期中) 如图，在平面直角坐标系内， $\text{[math]}$ 三个顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ （网格中每个小正方形的边长为1），以点O为位似中心，画出 $\text{[math]}$ 的位似图形 $\text{[math]}$ ，相似比为2．
1. （1）请在第一象限内画出 $\text{[math]}$ ；
2. （2）若以A，B，C，D为顶点的四边形是平行四边形，请直接写出满足条件的点D的坐标．
答案解析收藏纠错 + 选题
20. (2022九上·临汾期中) 阅读与思考
阅读下列材料，并完成相应的任务：
法国数学家爱德华•卢卡斯以研究斐波那契数列而著名，他曾给出了求斐波那契数列第n项的表达式，创造出了检验素数的方法，还发明了汉诺塔问题．“卢卡斯数列”是以卢卡斯命名的一个整数数列，在股市中有广泛的应用．卢卡斯数列中的第n个数 $\text{[math]}$ 可以表示为 $\text{[math]}$ ，其中 $\text{[math]}$ ．（说明：按照一定顺序排列着的一列数称为数列）
任务：
1. （1）卢卡斯数列中的第1个数 $\text{[math]}$ ，第2个数 $\text{[math]}$ ；
2. （2）卢卡斯数列有一个重要特征：当 $\text{[math]}$ 时，满足 $\text{[math]}$ ．请根据这一规律写出卢卡斯数列中的第6个数 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2022九上·临汾期中) 如图为幸福小区入口处安装的汽车出入道闸示意图．如图1，道闸关闭时，四边形 $\text{[math]}$ 是矩形．如图2，在道闸打开的过程中，边 $\text{[math]}$ 固定， $\text{[math]}$ 直线l，连杆 $\text{[math]}$ 、 $\text{[math]}$ 分别绕点A、D转动，且边 $\text{[math]}$ 始终与边 $\text{[math]}$ 平行，P为 $\text{[math]}$ 上的一点（不与点C，D重合），过点P作 $\text{[math]}$ 直线l， $\text{[math]}$ ，垂足分别为E，F，即四边形 $\text{[math]}$ 是矩形，过点D作 $\text{[math]}$ ，垂足为Q，延长 $\text{[math]}$ 与 $\text{[math]}$ 相交于点R．
1. （1） $\text{[math]}$ 与 $\text{[math]}$ 相似吗？请判断并说明理由．
2. （2）若道闸长 $\text{[math]}$ 米，宽 $\text{[math]}$ 米，点D距地面 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米．
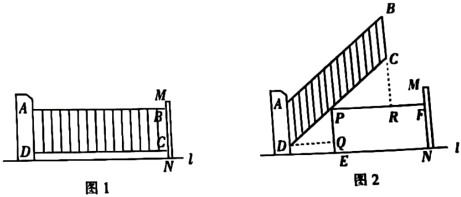
  ①求点B到地面l的距离；
  
  ②求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2022九上·临汾期中) 综合与实践
问题情境：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点B顺时针旋转得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点F．
1. （1）猜想验证：
  试猜想 $\text{[math]}$ 与 $\text{[math]}$ 是否相似？并证明你的猜想．
2. （2）探究证明：
  如图，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点H， $\text{[math]}$ 与 $\text{[math]}$ 相交于点G， $\text{[math]}$ 是否成立？并说明理由．
3. （3）拓展延伸：
  若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2022九上·临汾期中) 綜合与探究
如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点M从点A开始沿 $\text{[math]}$ 边向点C以 $\text{[math]}$ 的速度运动，点N从点C开始沿 $\text{[math]}$ 边向点B以 $\text{[math]}$ 的速度运动，当点M到达点C时，点M，N同时停止运动．若 $\text{[math]}$ ， $\text{[math]}$ 的长是 $\text{[math]}$ 的两根（其中 $\text{[math]}$ ，单位： $\text{[math]}$ ）．
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的长；
2. （2）如果点M，N分别从点A，C同时出发，那么几秒后， $\text{[math]}$ 的面积为 $\text{[math]}$ ？
3. （3）如果点M，N分别从点A，C同时出发， $\text{[math]}$ 是否能和 $\text{[math]}$ 相似？如果能，请求出运动的时间；如果不能，请说明理由．
答案解析收藏纠错 + 选题