 B .
B .  C .
C .  D .
D . 
|
时间/分钟 |
0 |
5 |
10 |
15 |
20 |
25 |
|
温度/℃ |
10 |
25 |
40 |
55 |
70 |
85 |
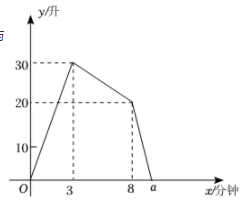
若温度的变化是均匀的,则14分钟时的温度是℃.
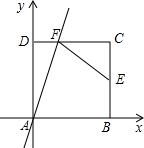


⑴请在图中画出ABC;
⑵将ABC向左平移5个单位,再沿x轴翻折得到
A1B1C1 , 请在图中画出
A1B1C1;
⑶若ABC 内有一点P(a,b),则点P经上述平移、翻折后得到的点P1的坐是 ▲ .


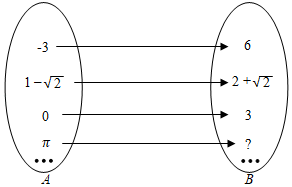
①在图1中, ▲
,
▲
;
②在图2中,求和
的交点H的坐标;