
 B .
B .  C .
C .  D .
D . 
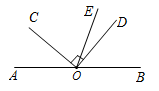


如图, ,
平分
,
平分
,
. 求证:
.

证明:∵平分
,
平分
, (已知)
∴ ▲ ,
▲ . (角平分线的定义)
又∵ , (已知)
∴∠ ▲ =∠ ▲ . (等量代换)
又∵ , (已知)
∴∠ ▲ ∠ ▲ . (等量代换)
∴ . ( )
进出数量(单位:吨) | -2 | 3 | -1 | 2 | -4 |
进出次数 | 2 | 1 | 3 | 4 | 2 |
方案一:运进每吨原料费用6元,运出每吨原料费用9元;
方案二:不管运进还是运出费用都是每吨7元.
从节约运费的角度考虑,请说明选择哪种方案比较合适.
在射线上画出点E,使C为线段
的中点,连接
.
定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的 , 则称该点是其他两个点的“倍分点”.例如,数轴上点A,B,C所表示的数分别为–1,0,2,且满足
, 则点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.

问题情境:
数学活动课上,老师展示了一个问题:如图1,直线 , 直线
与
,
分别交于点C,D,点A在直线
上,且在点C的左侧,点B在直线
上,且在点D的左侧,点Р是直线
上的一个动点(点Р不与点C,D重合).当点Р在点C,D之间运动时,试猜想
,
,
之间的数量关系,并说明理由.
独立思考:

勤学小组对此问题进行了更深一步的思考:当点Р在C,D两点的外侧运动时, ,
,
之间的数量关系又是如何?