
 B .
B .  C .
C .  D .
D . 
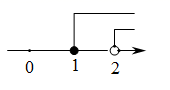 B .
B . 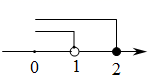 C .
C . 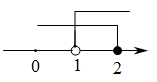 D .
D . 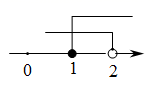

.甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组:
):
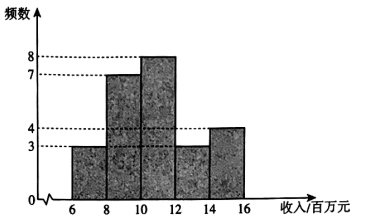
.甲城市邮政企业4月份收入的数据在
这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8
.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
| 平均数 | 中位数 | |
| 甲城市 | 10.8 | |
| 乙城市 | 11.0 | 11.5 |
根据以上信息,回答下列问题:

(参考数据: ,
,
,
,
,
)

