山西省晋城市高平市2021-2022学年八年级下学期期末质量...

更新时间：2024-07-13 浏览次数：89 类型：期末考试

一、单选题

1. (2022八下·高平期末) 若分式 $\text{[math]}$ 有意义，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八下·高平期末) 如图所示，四边形 $\text{[math]}$ 是平行四边形，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·廉江期末) 已知点 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图象上，则m与n的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
4. (2022八下·高平期末) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ，则 $\text{[math]}$ 的面积为（）

A . 9 B . 10 C . 11 D . 12

答案解析收藏纠错 + 选题
5. (2022八下·高平期末) 已知反比例函数 $\text{[math]}$ ，则下列描述错误的是（）

A . 图象位于第一，第三象限 B . 图像必经过点 $\text{[math]}$ C . 图象不可能与坐标轴相交 D . y随x的增大而减小

答案解析收藏纠错 + 选题
6. (2022八下·高平期末) 下面是一位同学做分式运算的过程，M，N代表代数式，则下列关于M、N的式子正确的是（）
$\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·黔江期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点E， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点F，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . 2 B . 1 C . 3 D . 3.5

答案解析收藏纠错 + 选题
8. (2022八下·高平期末) 新龟兔赛跑的故事：龟兔从同一地点同时出发后，兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先，就躺在路边呼呼大睡起来.当它一觉醒来，发现乌龟已经超过它，于是奋力直追，最后同时到达终点.用S₁、S₂分别表示乌龟和兔子赛跑的路程，t为赛跑时间，则下列图象中与故事情节相吻合的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2022八下·高平期末) 为了考察甲、乙两块地中小麦的长势，分别从中随机抽出10株麦苗，测得麦苗高如图所示，若 $\text{[math]}$ 和 $\text{[math]}$ 分别表示甲、乙两块地麦苗高数据的方差，则（）

A . $\text{[math]}$ ＝ $\text{[math]}$ B . $\text{[math]}$ ＜ $\text{[math]}$ C . $\text{[math]}$ ＞ $\text{[math]}$ D . 不确定

答案解析收藏纠错 + 选题
10. (2022八下·高平期末) 如图，在正方形 $\text{[math]}$ 中，点P在边 $\text{[math]}$ 上， $\text{[math]}$ 于点E， $\text{[math]}$ 于点F，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2023七下·吉林期末) 如图是一片枫叶标本，其形状呈“掌状五裂型”，裂片具有少数突出的齿．将其放在平面直角坐标系中，表示叶片“顶部”A，B两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，则叶杆“底部”点C的坐标为．

答案解析收藏纠错 + 选题
12. (2022八下·高平期末) 某校拟招聘一名优秀数学教师，现有甲、乙、丙三名教师入围，三名教师笔试、面试成绩如下表所示，综合成缋按照笔试占60%、面试占40%进行计算，学校录取综合成绩得分最高者，则被录取敦师的综合成绩为．
教师成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分

答案解析收藏纠错 + 选题
13. (2022八下·高平期末) 如图，E是平行四边形 $\text{[math]}$ 内任一点，若 $\text{[math]}$ ，则图中阴影部分的面积是．

答案解析收藏纠错 + 选题
14. (2022八下·高平期末) 如图，点A、C是反比例函数图象上的点，且关于原点对称．过点A作 $\text{[math]}$ 轴于点B，若 $\text{[math]}$ 的面积为7，则反比例函数的表达式为．

答案解析收藏纠错 + 选题
15. (2022八下·高平期末) 若点E是 $\text{[math]}$ 的中点， $\text{[math]}$ ，将正方形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点D恰好落在 $\text{[math]}$ 边的中点E处，点A的对应点为点P，则折痕 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2022八下·高平期末)
1. （1）计算： $\text{[math]}$
2. （2）先化简 $\text{[math]}$ ，再任意选取x代入求值．
答案解析收藏纠错 + 选题
17. (2022八下·高平期末) 如图：矩形 $\text{[math]}$ 的对角线相交于点O， $\text{[math]}$ ， $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是菱形．

答案解析收藏纠错 + 选题
18. (2022八下·高平期末) 为了解甲､乙两座城市的邮政企业4月份收入的情况，从这两座城市的邮政企业中，各随机抽取了25家邮政企业，获得了它们4月份收入（单位：百万元）的数据，并对数据进行整理､描述和分析．下面给出了部分信息．
$\text{[math]}$ ．甲城市邮政企业4月份收入的数据的频数分布直方图如下（数据分成5组： $\text{[math]}$ ）：

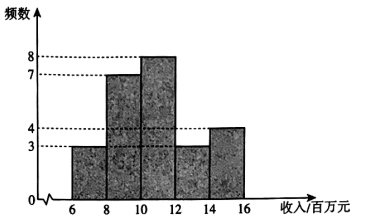
$\text{[math]}$ ．甲城市邮政企业4月份收入的数据在 $\text{[math]}$ 这一组的是：10.0，10.0，10.1，10.9，11.4，11.5，11.6，11.8

$\text{[math]}$ ．甲､乙两座城市邮政企业4月份收入的数据的平均数､中位数如下：

平均数

中位数

甲城市

10.8

$\text{[math]}$

乙城市

11.0

11.5

根据以上信息，回答下列问题：
1. （1）写出表中 $\text{[math]}$ 的值；
2. （2）在甲城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为 $\text{[math]}$ ．在乙城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为 $\text{[math]}$ ．比较 $\text{[math]}$ 的大小，并说明理由；
3. （3）若乙城市共有200家邮政企业，估计乙城市的邮政企业4月份的总收入（直接写出结果）．
答案解析收藏纠错 + 选题
19. (2022八下·高平期末) 1896年，挪威生理学家古德贝发现，每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点，这就导致每个人在蒙上眼晴行走时，虽然主观上沿某一方向直线前进，但实际上走出的是一个大圆圈，这就是有趣的“瞎转圈”现象．经研究，某人蒙上眼睛走出的大圆圈的半径y（米）是其两腿迈出的步长之差x（厘米）的反比例函数 $\text{[math]}$ ，其图象如图所示，请根据图象中的信息解决下列问题：
1. （1）求y与x之间的函数表达式；
2. （2）当某人两腿迈出的步长之差为0.25厘米时，他蒙上眼睛走出的大圆圈的半径为米；
3. （3）若某人蒙上眼睛走出的大圆圈的半径不小于70米，则其两腿迈出的步长之差最多是厘米．
答案解析收藏纠错 + 选题
20. (2023八下·霍州期中) 高平素有梨乡之称，高平大黄梨的甘酸适度，维生素、矿物质含量高，以黄梨为原料制成的梨干因食用方便更是受到了人们的青睐．某超市欲购进A、B两种袋装黄梨干，用160元购进的A种黄梨干与用240元购进的B种黄梨干的数量相同，每袋B种黄梨干的进价比A种黄梨干的进价贵10元．
1. （1）求A、B两种黄梨干每袋的进价分别为多少元？
2. （2）若该商店A种黄梨干每袋售价24元，B种黄梨干每袋售价35元，准备再次购进A，B两种黄梨干共100袋．在这100袋两种黄梨干全部售完的情况下，设购进A种黄梨干的数量为a袋，销售这两种黄梨干的利润为w元，写出w与a的函数关系式，若要保证售完后获利不低于468元，该商店该如何进货？
答案解析收藏纠错 + 选题
21. (2022八下·高平期末) 阅读下面材料，完成任务．
如图①，在等边三角形 $\text{[math]}$ 内有一点P，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的大小．
李明同学的思路是：将 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ ，画出旋转后的图形（如图②），连接 $\text{[math]}$ ，可得 $\text{[math]}$ 是等边三角形，而 $\text{[math]}$ 又是直角三角形（由勾股定理的逆定理可证），所以 $\text{[math]}$ ，则 $\text{[math]}$ ，
任务：
请你参考李明同学的思路，探究并解决下列问题：如图③，在正方形 $\text{[math]}$ 内有一点P，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
1. （1）求 $\text{[math]}$ 的大小；
2. （2）求正方形 $\text{[math]}$ 的边长．
答案解析收藏纠错 + 选题
22. (2022八下·高平期末) 综合与实践．如图①，四边形 $\text{[math]}$ 是矩形，且 $\text{[math]}$ ， $\text{[math]}$ ， O为矩形 $\text{[math]}$ 对角线的交点，E为 $\text{[math]}$ 边上任意一点，连结 $\text{[math]}$ 并延长，与 $\text{[math]}$ 边交于点F．
1. （1）观察：线段 $\text{[math]}$ 和 $\text{[math]}$ 有什么数量关系？并进行证明．
2. （2）操作：小英连结 $\text{[math]}$ 、 $\text{[math]}$ 后发现，四边形 $\text{[math]}$ 的形状一定是；当 $\text{[math]}$ 的长为时，四边形 $\text{[math]}$ 是菱形
3. （3）探究：受小英的启发，小亮对图形进一步操作，将图②中的 $\text{[math]}$ 与 $\text{[math]}$ 分别沿 $\text{[math]}$ 与 $\text{[math]}$ 进行翻折，点A与点C分别落在矩形 $\text{[math]}$ 内的点 $\text{[math]}$ 、 $\text{[math]}$ 处，连结 $\text{[math]}$ 、 $\text{[math]}$ ，如图③，请你判断四边形 $\text{[math]}$ 的形状，并证明你的结论．
答案解析收藏纠错 + 选题
23. (2022八下·高平期末) 综合与探究：直线 $\text{[math]}$ 与x轴和y轴分别交于点A、B，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点C，与y轴交于点 $\text{[math]}$ ，过点C作 $\text{[math]}$ 轴于点E，点E的横坐标为3．
1. （1）求直线 $\text{[math]}$ 的解析式；
2. （2）点P是x轴上一动点，过点 $\text{[math]}$ 作x轴垂线分别与直线 $\text{[math]}$ 、 $\text{[math]}$ 交于点M、N，求线段 $\text{[math]}$ 的长（用t表示）；
3. （3）在（2）的条件下，t为何值时，以M、N、C、E为顶点的四边形是平行四边形．
答案解析收藏纠错 + 选题