题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

贵州省遵义市桐梓县私立达兴中学2021-2022学年八年级下...

更新时间：2024-07-31 浏览次数：28 类型：月考试卷

一、单选题

1. (2022八下·桐梓月考) 下列四个数中，是负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八下·桐梓月考) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022八下·桐梓月考) 截至2020年5月4日，海外新冠肺炎确诊病例累计逾349.5万例，数349.5万用科学记数法表示为（）

A . 3.495×10⁶ B . 34.95×10⁵ C . 3.495×10⁵ D . 0.3495×10⁷

答案解析收藏纠错 + 选题
4. (2022八下·桐梓月考) 下列各式中，不一定是非负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·桐梓月考) 以方程组 $\text{[math]}$ 的解为坐标的点（x，y）在平面直角坐标系中的位置是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
6. (2022八下·桐梓月考) 下列图形中既不是轴对称图形也不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2024八上·洪山月考) 一个多边形的内角和是外角和的3倍，这个多边形的边数是（）

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
8. (2022八下·桐梓月考) 函数y＝ $\text{[math]}$ 自变量x的取值范围是（）

A . x≠3 B . x≤5 C . x≤5且x≠3 D . x＜5且x≠3

答案解析收藏纠错 + 选题
9. (2022八下·桐梓月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八下·阿荣旗月考) 如果实数 $\text{[math]}$ 满足 $\text{[math]}$ ，那么点 $\text{[math]}$ 在（）.

A . 第一象限 B . 第二象限 C . 第二象限或坐标轴上 D . 第四象限或坐标轴上

答案解析收藏纠错 + 选题
11. (2022八下·桐梓月考) 如图，等边△ABC的边长为2，AD是BC边上的高，则高AD的长为（）

A . .1 B . . $\text{[math]}$ C . $\text{[math]}$ D . .2

答案解析收藏纠错 + 选题
12. (2022八下·桐梓月考) 适合下列条件的 $\text{[math]}$ 中，直角三角形的个数为（）
① $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ .⑥ $\text{[math]}$

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题

二、填空题

13. (2022八下·桐梓月考) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2022八下·桐梓月考) 若最简根式 $\text{[math]}$ 与 $\text{[math]}$ 是同类二次根式，则m＝．

答案解析收藏纠错 + 选题
15. (2022八下·桐梓月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线，若 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的最小值是

答案解析收藏纠错 + 选题

三、解答题

16. (2022八下·桐梓月考) 如图，学校操场边上一块空地（阴影部分）需要绿化，连接AC，测出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求需要绿化部分的面积．

答案解析收藏纠错 + 选题
17. (2022八下·桐梓月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2022八下·桐梓月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2022八下·桐梓月考) 如图所示，点E在△ABC外部，点D在BC边上，DE交AC于F，若∠1=∠3，∠E=∠C，AE=AC，求证：△ABC≌△ADE.

答案解析收藏纠错 + 选题
20. (2022八下·桐梓月考) 根据疫情防控工作需要，某社区组织甲、乙两支医疗队开展疫苗接种工作，甲队比乙队每小时多接种30人，甲队接种2250人与乙队接种1800人用时相同，问甲队每小时接种多少人？

答案解析收藏纠错 + 选题
21. (2022八下·桐梓月考) $\text{[math]}$ ， $\text{[math]}$ 两个果园分别有苹果 $\text{[math]}$ 吨和 $\text{[math]}$ 吨， $\text{[math]}$ 、 $\text{[math]}$ 两城市分别需要苹果 $\text{[math]}$ 吨和 $\text{[math]}$ 吨；已知从 $\text{[math]}$ 、 $\text{[math]}$ 到 $\text{[math]}$ 、 $\text{[math]}$ 的运价如下表：

到 $\text{[math]}$ 城市
到 $\text{[math]}$ 城市
$\text{[math]}$ 园
每吨15元
每吨12元
$\text{[math]}$ 园
每吨10元
每吨9元
1. （1）若从 $\text{[math]}$ 果园运到 $\text{[math]}$ 城的苹果为 $\text{[math]}$ 吨，则从 $\text{[math]}$ 果园运到 $\text{[math]}$ 城的苹果为吨，从 $\text{[math]}$ 果园将苹果运往 $\text{[math]}$ 的运输费用为吨.
2. （2）用含 $\text{[math]}$ 的式子表示出总运输费.（要求：先列式，再化简）
3. （3）当 $\text{[math]}$ 时，总运输费用为多少元？
答案解析收藏纠错 + 选题
22. (2022八下·桐梓月考) 如图，在△ABC中，AB＝10 $\text{[math]}$ m，BC＝40m，∠C＝90°，点P从点A开始沿边AC边向点C以2m/s的速度匀速移动，同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动，几秒时，△PCQ的面积等于432m²？

答案解析收藏纠错 + 选题
23. (2022八下·桐梓月考) 如图是美国总统Garfield于1876年给出的一种验证勾股定理的办法，你能利用它证明勾股定理吗？请写出你的证明过程.（提示：如图三个三角形均是直角三角形）

答案解析收藏纠错 + 选题
24. (2022八下·桐梓月考) 课堂上同学们正在讨论课本例题：如图，一架 $\text{[math]}$ 长的梯子 $\text{[math]}$ 斜靠在竖直的墙 $\text{[math]}$ 上， $\text{[math]}$ 的距离为 $\text{[math]}$ ，若梯子顶端下滑的距离为 $\text{[math]}$ ，则点 $\text{[math]}$ 向外移动的距离为多少？

同学甲：本题可以这样来做

解：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，根据勾股定理得：

$\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ，

又在 $\text{[math]}$ 中， $\text{[math]}$ ，根据勾股定理得：

$\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .

同学乙.我发现在本题答案中，梯子顶端下滑的距离 $\text{[math]}$ 比末端向外移动的距离 $\text{[math]}$ 小，说明在梯子下滑时，梯子顶端下滑的距离一定比末端向外移动的距离小.

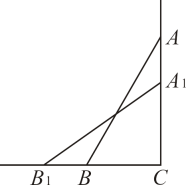
同学丙：不一定，我能举个反例，比如，当梯子顶端下滑的距离为 $\text{[math]}$ 时，

在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，根据勾股定理得： $\text{[math]}$ $\text{[math]}$ ，则

$\text{[math]}$ ，

又在 $\text{[math]}$ 中， $\text{[math]}$ ，根据勾股定理得：

$\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .即： $\text{[math]}$ ，

老师.通过上面的讨论，同学们发现有时 $\text{[math]}$ 大，有时 $\text{[math]}$ 大，那么有没有可能正好 $\text{[math]}$ 的情况存在呢？

同学丁：有.当梯子顶端从 $\text{[math]}$ 处下滑 $\text{[math]}$ 时，末端向外也移动 $\text{[math]}$ .你认为他的说法正确吗？说明理由.

答案解析收藏纠错 + 选题

试卷信息