黑龙江省齐齐哈尔富拉尔基区2022年九年级三模数学试题

更新时间：2023-03-28 浏览次数：43 类型：中考模拟

一、单选题

1. (2022·富拉尔基模拟) -2022的相反数是（）

A . 2022 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·富拉尔基模拟) 下列图形中，既是中心对称图形，又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·富拉尔基模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·富拉尔基模拟) 甲口袋中有2个白球、1个红球，乙口袋中有1个白球、1个红球，这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.下列事件中，概率最大的是（）

A . 摸出的2个球颜色相同 B . 摸出的2个球颜色不相同 C . 摸出的2个球中至少有1个红球 D . 摸出的2个球中至少有1个白球

答案解析收藏纠错 + 选题
5. (2022·富拉尔基模拟) 将一副三角板按照如图所示的位置摆放在直尺上，则 $\text{[math]}$ 的度数为（）

A . 105° B . 115° C . 120° D . 135°

答案解析收藏纠错 + 选题
6. (2022·富拉尔基模拟) 星期日早晨，小明从家匀速跑到公园，在公园某处停留了一段时间，再沿原路匀速步行回家，小明离公园的路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的关系的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022·富拉尔基模拟) 由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示，则搭建这个几何体所需要的小正方体的个数至少为（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
8. (2022·富拉尔基模拟) 为了庆祝中国共青团100周年诞辰，某校将举办“激情五月，青春心向党”为主题的演讲比赛活动，计划用80元钱购买甲、乙两种水晶奖杯作为奖品（两种都买）已知甲种奖杯每个8元，乙种奖杯每个12元，则购买水晶奖杯的方案共有（）

A . 3种 B . 4种 C . 5种 D . 6种

答案解析收藏纠错 + 选题
9. (2022·富拉尔基模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使 $\text{[math]}$ ，连接CE，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·富拉尔基模拟) 如图，抛物线 $\text{[math]}$ $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ．有下列五个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤若 $\text{[math]}$ 为关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个根，则 $\text{[math]}$ ．你认为其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

11. (2022·富拉尔基模拟) 新型冠状病毒的直径平均为100纳米， $\text{[math]}$ ，将110纳米用科学记数法表示为米．

答案解析收藏纠错 + 选题
12. (2022·富拉尔基模拟)
如图，在△ABC中，点D，E，F分别是边BC，CA，AB的中点，使四边形AFDE为菱形，应添加的条件是（添加一个条件即可）．

答案解析收藏纠错 + 选题
13. (2024九下·青田模拟) 用半径为 $\text{[math]}$ ，圆心角为 $\text{[math]}$ 的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2022·富拉尔基模拟) 关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 的解为非负数，则 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题
15. (2022·富拉尔基模拟) 如图，A、B是反比例函数y＝ $\text{[math]}$ （k>0）图象上的点，A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S_△AOC＝6．则k＝．

答案解析收藏纠错 + 选题
16. (2022·富拉尔基模拟) 矩形一个内角的平分线分矩形的一边为3cm和5cm两部分，则这个矩形的面积为cm² ．

答案解析收藏纠错 + 选题
17. (2022·富拉尔基模拟) 如图，在平面直角坐标系中，点A₁、A₂、A₃…在直线y=x+1上，以OA₁为边作第一个正方形OA₁B₁C₁ ，使点C₁在x轴的正半轴上，得到正方形OA₁B₁C₁的对角线的交点G₁；以C₁A₂为边作第二个正方形C₁A₂B₂C₂ ，使点C₂在x轴的正半轴上，得到正方形C₁A₂B₂C₂的对角线的交点G₂；依次作下去，则第2022个正方形C₂₀₂₁A₂₀₂₂B₂₀₂₂C₂₀₂₂的对角线的交点G₂₀₂₂的坐标是．

答案解析收藏纠错 + 选题

三、解答题

18. (2022·富拉尔基模拟)
1. （1）计算： $\text{[math]}$
2. （2）分解因式： $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2024九上·鹿寨期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022·富拉尔基模拟) 为了贯彻落实“双减”政策，丰富课后服务内容，满足学生的个性发展需求，齐齐哈尔市某校推出多元课程，助力学生成长．为了解同学们对多元课程的喜欢程度，抽取部分学生进行调查．被调查的每个学生按A（非常喜欢）、B（比较喜欢）、C（一般喜欢）、 D（不喜欢）四个等级对活动进行评价．图①和图②是采集数据后绘制的两幅统计图、条形统计图有一处错误且不完整，扇形统计图是正确的

请你根据统计图提供的信息，解答下列问题：
1. （1）此次调查的学生有人；表示“非常喜欢”所对应扇形的圆心角度数是；
2. （2）条形统计图中存在错误的是（填A、B、C中的一个），此等级正确人数为人；
3. （3）将图①条形统计图中的D等级补充完整；
4. （4）若该校约有3000名学生，请估计“非常喜欢”和“比较喜欢”的学生共约有多少人？
答案解析收藏纠错 + 选题
21. (2022·富拉尔基模拟) 如图，AB是⊙O的直径，点C是⊙O上一点（与点A，B不重合），过点C作直线PQ，使得∠ACQ＝∠ABC.
1. （1）求证：直线PQ是⊙O的切线.
2. （2）过点A作AD⊥PQ于点D，交⊙O于点E，若⊙O的半径为2，sin∠DAC＝ $\text{[math]}$ ，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
22. (2022·富拉尔基模拟) 一辆快车从甲地驶往乙地，到达乙地后立刻返回甲地，同时一辆慢车从乙地驶往甲地，到达甲地后停止行驶，已知两车相遇时快车比慢车多行驶40千米．设行驶时间为x（单位：小时），两车之间的距离为y（单位：千米），y与x之间的函数关系如图，
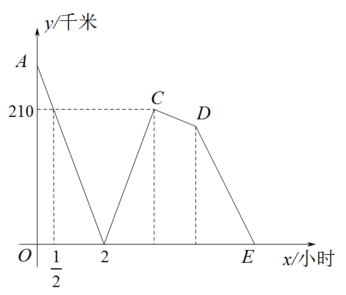
根据图象解答下列问题：
1. （1）直接写出快、慢两车的速度；
2. （2）求快车从乙地返回甲地的过程中y与x的函数解析式；
3. （3）直接写出何时两车相距70千米．
答案解析收藏纠错 + 选题
23. (2022·富拉尔基模拟) 综合与实践
如图①，Rt△ABC中，∠ACB= 90° ，CD为Rt△ABC的斜边上的中线，在证明CD=AD= BD的过程中，我们可以延长CD到E，使得CD=DE ，连接BE．很容易证明∠ACD≌△BED，进而证明△ABC≌△ECB，所以AB=CE，所以CD= AD= BD．我们可以得到直角三角形的性质：直角三角形斜边中线等于斜边的一半．
实践操作：将两个全等的Rt△ABD，Rt△ACE拼在一起，如图②，△ABD不动．
1. （1）问题解决：将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB，MC，如图③，求证：MB=MC；
2. （2）拓展延伸：若将图②中的CE向上平移，且∠CAE不变，连接DE ，M是DE的中点，连接MB ，MC，如图④，则线段MB，MC的数量关系为；
3. （3）问题再探：在（2）的条件下，若∠CAE改变大小，如图⑤，其他条件不变，请你判断线段MB ，MC的数量关系还成立吗?请说明理由．
答案解析收藏纠错 + 选题
24. (2022·富拉尔基模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于A （-3，0）、B （4，0）两点，与y轴交于点C．
1. （1）求抛物线解析式；
2. （2）点H是抛物线对称轴上的一个动点，连接AH、CH，直接写出△ACH周长的最小值为；
3. （3）若点G是第四象限抛物线上的动点，求△BCG面积的最大值以及此时点G的坐标；
4. （4）若点M是∠BAC平分线上的一点，点N是平面内一点，若以A、B、M、N为顶点的四边形是矩形，请直接写出点N坐标．
答案解析收藏纠错 + 选题