
两点之间的距离公式
如果数轴上的点 ,
分别表示实数
,
, 两点
,
间的距离记作
, 那么
.
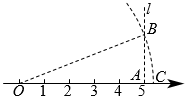
对于平面上的两点 ,
间的距离是否有类似的结论呢?
运用勾股定理,就可以推出平面上两点之间的距离公式.
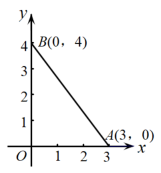
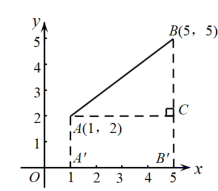
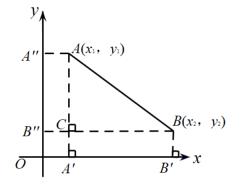
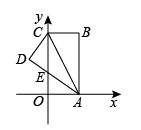
对于问题3,作轴,
轴,垂足分别为点
,
;作
轴,垂足为
;作
, 垂足为点C,且延长BC与y轴交于点
, 则四边形
,
是长方形.
∵,
,
∴.
∴ .
这就是平面直角坐标系中两点之间的距离公式.
,
;
材料一:把分母中的根号化去,使分母转化为有理数的过程,叫做分母有理化通常把分子、分母乘以同一个不等于0的式子,以达到化去分母中根号的目的
例如:化简
解:
材料二:化简的方法:如果能找到两个实数m,n,使
, 并且
,
那么
例如:化简
解:
填空:化简的结果等于;
①;
② .
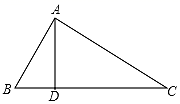
①如图2,当点N恰好在 边上时,求证:
;
②当点 在同一条直线上时,若
,请直接写出线段
的长.