![]()

 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 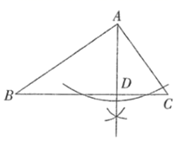
 B .
B . 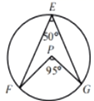 C .
C . 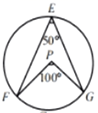 D .
D . 



解:
|
①小颖解方程的方法是;
②第二步变形的依据是;
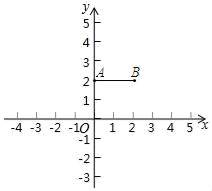
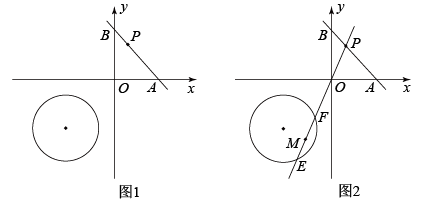
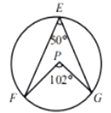
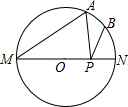
【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,
于点C,点D在弦
上且
, 在弧
上取一点Q,使弧
=弧
, 连接
, 则有
.