山西省大同市云冈区2022年九年级中考二模数学试题

更新时间：2023-03-29 浏览次数：84 类型：中考模拟

一、单选题

1. 计算 $\text{[math]}$ 的结果是（）

A . -6 B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 将一个六角螺母按如图所示的方式摆放，则它的主视图正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 1月27日，山西省住建厅消息，去年我省大力实施城市更新，城市人居环境不断改善，新增城市绿地1356万平方米、绿道110公里、公园及小微绿地162个，城市生态环境进一步改善．数据“1356万”用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 将一个直角三角板和一把直尺按如图所示摆放，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 已知实数x，y，若 $\text{[math]}$ ，则下列结论中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 下表是我省6个市今年某日的最高气温（℃）的统计结果：
城市
太原市
运城市
晋中市
吕梁市
临汾市
朔州市
气温（℃）
13
16
12
12
15
12
则该日最高气温（℃）的众数和中位数分别是（）

A . 12，13 B . 12，12.5 C . 16，12 D . 12，12

答案解析收藏纠错 + 选题
8. 小明和小亮相约到汾河公园健身步道上参加健步走活动，他们同时同地出发，线路长度为8公里．已知小明的速度是小亮的1.5倍，小明比小亮提前12分钟走完全程，设小亮的速度为xkm/h，则下列方程中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图，CA，CB分别与⊙O相切于点A，B． $\text{[math]}$ ，点D是⊙O上一点，则∠D的度数为（）

A . 122° B . 61° C . 58° D . 60°

答案解析收藏纠错 + 选题
10. 如图，在平面直角坐标系中，点A是y轴上一动点，点B是x轴上一定点，点B的坐标为 $\text{[math]}$ ，四边形ABCD是以AB为边的正方形，设点A的纵坐标为a，则点C的坐标可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 因式分解 $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题
12. 我国北方有一个习俗：过年包饺子时会随机在饺子中包上糖果或硬币，我们称其为“幸运饺子”．吃到“幸运饺子”的人新的一年的日子会甜甜美美、万事如意．小亮家在大年初一时共煮了50个饺子，其中有4个“幸运饺子”，小亮从中随机挑选了一个饺子正好是“幸运饺子”的概率是．

答案解析收藏纠错 + 选题
13. 如图，已知A点是反比例函数 $\text{[math]}$ （k≠0）的图象上一点，AB⊥y轴于B，且 $\text{[math]}$ ABO的面积为3，则k的值为．

答案解析收藏纠错 + 选题
14. 将一组数按如下规律排列：
则第10行的第3个数是．

答案解析收藏纠错 + 选题
15. 如图，Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， CD平分∠ACB，点E是AC边上的中点，连接BE，与CD交于点M，则EM的长为．

答案解析收藏纠错 + 选题

三、解答题

16. 计算题：
1. （1）计算 $\text{[math]}$ ：
2. （2）先化简，再求值 $\text{[math]}$ ，其中 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）请调出将△ABC向左平移4个单位长度，再向上平移1个单位长度后得到的 $\text{[math]}$ ；
2. （2）请画出与△ABC关于原点对称的 $\text{[math]}$ ；
3. （3）直接写出 $\text{[math]}$ ， $\text{[math]}$ 两点的坐标．
答案解析收藏纠错 + 选题
18. 第24届冬奥会于今年2月份在我国北京市和张家口市顺利举行，这是中国历史上第一次举办冬季奥运会．随着冬奥会的成功举办，冰雪运动在全国各地也得到了进一步音及和发展．依托这一良好契机，我省某中学组织了以“走入冰雪，享受快乐”为主题的冰雪知识竞赛，并随机抽取了部分学生的竞赛成绩（百分制）进行整理和分析（将分数分为四组：A． $\text{[math]}$ ， B． $\text{[math]}$ ， C． $\text{[math]}$ ， D． $\text{[math]}$ ），下面给出了部分信息：
抽取的学生竞赛成绩分布表
级别
分数/分
频数
A
$\text{[math]}$
a
B
$\text{[math]}$
12
C
$\text{[math]}$
6
D
$\text{[math]}$
3
请解答下列问题：
1. （1）直接写出a的值是、B所占的百分比是；
2. （2）该校共有300名学生参加了此次冰雪知识竞赛活动，估计在本次活动中取得分数在80分及以上的有多少人？
3. （3）学校计划从在本次竞赛中获得高分的小明，小亮，小颖和小白四名同学中随机选择两名同学作为宣传讲解员，为同学们科普冰雪运动的相关知识，请你用树状图或列表的方法求出小明和小颖被同时选中的概率．
答案解析收藏纠错 + 选题
19. 如图，四边形ABCD是平行四边形 $\text{[math]}$ 于点E， $\text{[math]}$ 于点F，连接AF和CE．
1. （1）证明：四边形AECF是平行四边形；
2. （2）已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 求CE的长．
答案解析收藏纠错 + 选题
20. 为庆祝新年，太原古县城举办了“锦绣太原中国年·风舞龙城花灯会”活动．此次花灯会利用彩灯工艺中的“行、色、声、光、动”特点，充分展现三晋人文特色、传统民俗．本次花灯会的票价公示如下表所示：
票价
1月25日-1月31日
2月1日-2月16日
2月17日-3月5日
成人票价
108元/人
180元/人
108元/人
优惠票价
50元/人
50元/人
50元/人
注：65周岁及以上的老年人，残疾人可按优惠票价购票，1.5米以下的儿童免费．
亮亮家和其他两个家庭共计10人（都需购票）于1月28日去太原古县城观赏花灯．亮亮按上面的收费标准计算出他们共需花费906元来购买门票．
1. （1）求他们需购买成人票和优惠票各多少张？
2. （2）后来，亮亮发现太原古县域还推出了200元的双人票优惠活动，请你帮他设计一种购票方案，使得购票费用最低，并求出最低费用是多少？
答案解析收藏纠错 + 选题
21. 北京冬奥会期间，首钢滑雪大跳台因其“玉如意”的绝美造型，高水平赛道的精修和维护工作受到了各国参赛运动员的盛赞．下图是一条滑雪赛道的简化示意图，它主要由跳台、助滑道和着陆坡三部分组成，已知点B与点C间的高度差为32米，着陆坡CD的倾斜角 $\text{[math]}$ 为37°，参赛运动员们将从点D处出发，乘车沿水平方向行驶至点E处，再沿斜坡EF行驶26米至点F处，最后乘坐垂直于水平方向的电梯到达点A处．已知斜坡EF的坡比为1：2.4，电梯AF的高度为50米，求着陆坡CD的长度，（结果精确到1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
22. 综合与实践
在一次综合实践活动课上，数学王老师给每位同学各发了一张正方形纸片，要求同学们仅通过折纸的方法来确定该正方形一边上的一个三等分点．
“启航”小组的同学在经过一番思考和讨论交流后，进行了如下的操作：
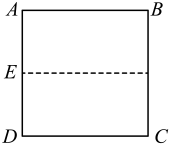
第一步：如图1，将正方形纸片ABCD的一条边AD对折，使点A和点D重合，得到AD的中点E，然后展开铺平；
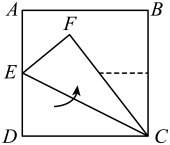
第二步：如图2，将CD边沿CE翻折到CF的位置；
第三步：如图3，再将BC沿过点C的直线翻折，使点B和点F重合，折痕与AB边交于点G．
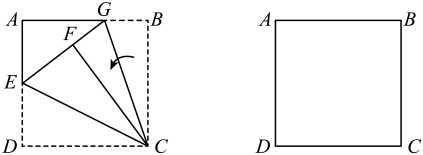
他们认为：该点G就是AB边的一个三等分点．
1. （1）试证明上面的结论：
2. （2） “奋进”小组的同学是这样操作的：
  第一步：先将正方形纸片ABCD的一条边AD对折，使点A和点D重合，找到AD的中点E；
  第二步：再折出正方形纸片ABCD的对角线AC，以及点B和点E的连线BE，这两条折痕相交于点F；
  第三步：最后，过点F折出AB的平行线GN，分别与AD，BC交于点G和点N．
  ①请根据上面的描述，在图4中画出所有的折痕，确定点G和点N的位置；
  ②请结合①中所画的图形，判断点G是否为AD边的三等分点，并说明理由．
答案解析收藏纠错 + 选题
23. 如图，已知抛物线 $\text{[math]}$ 与x轴相交于A，B两点（点A在点B左侧），与y轴交于点C．直线l与抛物线交于B，D两点，且点D的坐标为 $\text{[math]}$ ．直线m是抛物线的对称轴，与直线l交于点M．
1. （1）求点A，C两点的坐标及直线l的表达式；
2. （2）如图，点E，F是直线m上的两个动点（点F在点E下方），且 $\text{[math]}$ ，连接AD，DE，AF．求四边形ADEF周长的最小值；
3. （3）在直线m上是否存在一点P，使得△BDP为直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题