浙江省舟山市定海二中2022-2023学年九年级下学期3月份...

更新时间：2024-07-31 浏览次数：79 类型：月考试卷

一、选择题（每小题3分，每小题仅有一个正确选项，共30分．）

1. (2023九下·定海月考) 2023的绝对值为（）

A . 2023 B . -2023 C . 2023 D . -2023

答案解析收藏纠错 + 选题
2. (2023九下·定海月考) 一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9．这5个数据的众数是（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
3. (2023九下·舟山月考) 下列图形中，既是中心对称图形，又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023九下·定海月考) “多少事，从来急；天地转，光阴迫．一万年太久，只争朝夕．”伟人毛泽东通过这首《满江红·和郭沫若同志》告诉我们青年学生：要珍惜每分每秒；努力工作，努力学习.一天时间为86400秒，用科学记数法表示这一数字是

A . 864×10² B . 86.4×10³ C . 8.64×10⁴ D . 0.0.864×10⁵

答案解析收藏纠错 + 选题
5. (2023九下·定海月考) 如图，⊙O的直径CD垂直弦AB于点E，且CE=2， DE=8，则AB的长为（）

A . 4 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
6. (2023九下·定海月考) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九下·舟山月考) 如图，将ΔABC沿BC方向平移3cm得到ΔDEF，若ΔABC的周长为16cm，则四边形ABFD的周长为（）

A . 18cm B . 20cm C . 22cm D . 24cm

答案解析收藏纠错 + 选题
8. (2023九下·定海月考) 一个圆锥的侧面展开图是半径为6的半圆，则这个圆锥的底面半径为（ )

A . 3 B . 3.5 C . 4 D . 4.5

答案解析收藏纠错 + 选题
9. (2023九下·定海月考) 如图，在一张矩形纸片ABCCD中，AD=4cm，点E，F分别是CD和AB的中点.现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH.若HG的延长线恰好经过点D，则CD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九下·定海月考) 当 $\text{[math]}$ 时，二次函数 $\text{[math]}$ 有最大值4，则实数m的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共24分）

11. (2023九下·定海月考) 分解因式： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2023九下·定海月考) 一个正多边形的每个内角都为135°，那么该正多边形的边数为．

答案解析收藏纠错 + 选题
13. (2023九下·定海月考) 在 $\text{[math]}$ +（）=0的括号中添加一个实数，使方程有两个相等的实数根。

答案解析收藏纠错 + 选题
14. (2023九下·定海月考) 如图，在ΔABC中，AB=2 AC=4，将ΔABC绕点C按逆时针方向旋转得到ΔA'B'C使CB'//AB，分别延长AB，CA＇相交于点D，则线段BD的长为。

答案解析收藏纠错 + 选题
15. (2023九下·定海月考) 如图，把平面内一条数轴x绕原点O逆时针旋转角θ（(0°<θ<90°)）得到另一条数轴y，x轴和y轴构成一个平面斜坐标系.规定：过点P作y轴的平行线，交x轴于点A，过点P作x轴的平行线，交y轴于点B，若点A在x轴上对应的实数为a，点B在y轴上对应的实数为b，则称有序实数对，b）为点P的斜坐标，在某平面斜坐标系中，已知θ=60°点M的斜坐标为（3，2），点N与点M关于y轴对称，则点N的斜坐标为。

答案解析收藏纠错 + 选题
16. (2023九下·定海月考) 如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F.则下列结论：①CE=CF；②线段EF的最小值为 $\text{[math]}$ ；③若点F恰好落在弧BC上，则AD= $\text{[math]}$ ④当AD=2时，与半圆相切；⑤当点D从点A运动到点B时，线段 EF扫过的面积是 $\text{[math]}$ 。其中正确结论的序号是。

答案解析收藏纠错 + 选题

三、解答题（第17～18题每小题6分，第19题8分，第20题6分，第21题8分，第22，23题每小题10分，第24题12分，共66分）

17. (2023九下·定海月考) 计算
1. （1） $\text{[math]}$
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023九下·定海月考) 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简. 过程如图所示：
1. （1）接力中，自己负责的一步出现错误的同学是；
2. （2）请你书写正确的化简过程，并在“-1，0，1”中选择一个合适的数代入求值.
答案解析收藏纠错 + 选题
19. (2023九下·定海月考) 央视“经典咏流传”开播以来受到社会广泛关注。我校就“中华文化我传承-地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图。请你根据统计图所提供的信息解答下列问题：
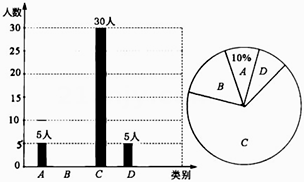
图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”。
1. （1）被调查的总人数是人，扇形统计图中C部分所对应的扇形圆心角的度数为.
2. （2）补全条形统计图；
3. （3）若我校共有学生1800人，请根据上述调查结果，估计该校学生中A类有人；
4. （4）在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率。
答案解析收藏纠错 + 选题
20. (2023九下·舟山月考) 已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF.
1. （1）求证：ΔDOE≌ΔBOF.
2. （2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由.
答案解析收藏纠错 + 选题
21. (2023九下·定海月考) 随着科技的发展，无人机已广泛应用于生产和生活，如代替人们在高空测量距离和角度，某校“综合与实践”活动小组的同学要测量AB，CD两座楼之间的距离，他们借助无人机设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为60m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24m到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内．请根据以上数据求楼AB与CD之间的距离AC的长（结果精确到1m．参考数据：sin 70°≈0.94 cos 70°≈0.34 tan 70°≈2.75， $\text{[math]}$ ≈1.73)

答案解析收藏纠错 + 选题
22. (2023九下·舟山月考) 某文具店最近有A，B两款纪念册比较畅销．该店购进A款纪念册5本和B款纪念册4本共需156元，购进A款纪念册3本和B款纪念册5本共需130元．在销售中发现：A款纪念册售价为32元／本时，每天的销售量为40本，每降低1元可多售出2本；B款纪念册售价为22元／本时，每天的销售量为80本，B款纪念册每天的销售量与售价之间满足一次函数关系，其部分对应数据如下表所示：

售价（元／本）

……

22

23

24

25

……

每天销售量（本）

……

80

78

76

74

……
1. （1）求A，B两款纪念册每本的进价分别为多少元？
2. （2）该店准备降低每本A款纪念册的利润，同时提高每本B款纪念册的利润，且这两款纪念册每天销售总数不变，设A款纪念册每本降价m元；
  ①直接写出B款纪念册每天的销售量（用含m的代数式表示）；
  
  ②当A款纪念册售价为多少元时，该店每天所获利润最大，最大利润是多少？
答案解析收藏纠错 + 选题
23. (2023九下·舟山月考) 已知抛物线 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求该抛物线与 $\text{[math]}$ 轴公共点的坐标；
2. （2）若 $\text{[math]}$ ，且当 $\text{[math]}$ 时，抛物线与x轴有且只有一个公共点，求 $\text{[math]}$ 的取值范围；
3. （3）若 $\text{[math]}$ ，且 $\text{[math]}$ 时，对应的 $\text{[math]}$ ； $\text{[math]}$ 时，对应的 $\text{[math]}$ ，试判断当 $\text{[math]}$ 时，抛物线与 $\text{[math]}$ 轴是否有公共点？若有，请证明你的结论；若没有，请说明理由.
答案解析收藏纠错 + 选题
24. (2023九下·定海月考) 如图，已知P为锐角∠MAN内部一点，过点P作PB⊥AM于点B，PC⊥AN于点C，以PB为直径作⊙O，交直线CP于点D，连接AP，BD，AP交⊙O于点E.
1. （1）求证：∠BPD=∠BAC.
2. （2）连接EB，ED，当 tan∠MAN=2 AB= $\text{[math]}$ 时，在点P的整个运动过程中.
  ①若∠BDE=45°，求PD的长.
  
  ②若ΔBED为等腰三角形，求直接写出所有满足条件的BD的长.
3. （3）连接OC，EC，OC交AP于点F，当tan∠MAN=1，OC∥BE时，记ΔOFPP的面积为S₁ ， ΔCFE 的面积为S₂ ，请求出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题