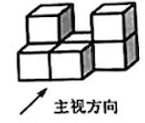
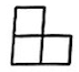
 B .
B . 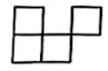 C .
C . 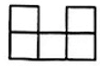 D .
D . 
 B .
B .  C .
C .  D .
D . 
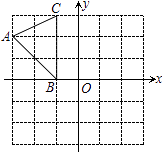
如图,在平面直角坐标系中,A(﹣3,2)、B(﹣1,0)、C(﹣1,3),将
△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1 , 点A、B、C的
对应点分别A1、B1、C1 , 则点A1的坐标为( )


某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )

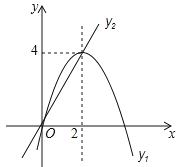
在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣或x=1.其中正确的有( )
![]()
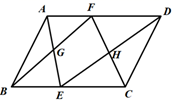

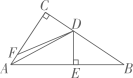

已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.

