山东省威海市2022年中考数学模拟试题

更新时间：2023-04-21 浏览次数：49 类型：中考模拟

一、单选题

1. (2024九下·凉州模拟) 计算下列各式，其结果为负数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·威海模拟) 如图是一个由6个相同的正方体组成的立体图形，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·威海模拟) 下列说法正确的是（）

A . 有两个内角相等的三角形不是轴对称图形 B . 如果两条线段互相垂直平分，那么这两条线段互为对称轴 C . 所有直角三角形都不是轴对称图形 D . 两个图形成轴对称，那么这两个图形全等

答案解析收藏纠错 + 选题
4. (2024七下·武昌月考) 在平面直角坐标系中，点M（﹣2，1）在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2022·威海模拟) 计算 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·威海模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·威海模拟) 若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根，则 $\text{[math]}$ 的值不能是（）

A . 2 B . 0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·威海模拟) 下列说法正确的是（）

A . 三角形的外角一定大于它的内角 B . 甲、乙两射击运动员分别射击10次，他们成绩的方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，这过程中乙发挥比甲更稳定 C . 8，9，10，11，11这组数的众数是2 D . 两个图形位似也一定相似

答案解析收藏纠错 + 选题
9. (2022·威海模拟) 某校举行春季运动会，需要在初一年级选取一名志愿者．初一（1）班、初一（2）班、初一（3）班各有2名同学报名参加．现从这6名同学中随机选取一名志愿者，则被选中的这名同学恰好是初一（3）班同学的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·威海模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，利用尺规在 $\text{[math]}$ ， $\text{[math]}$ 上分别截取 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ；分别以D，E为圆心、以大于 $\text{[math]}$ 为长的半径作弧，两弧在 $\text{[math]}$ 内交于点F；作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点G，若 $\text{[math]}$ ，P为 $\text{[math]}$ 上一动点，则 $\text{[math]}$ 的最小值为（）

A . 无法确定 B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题

二、填空题

11. (2022·威海模拟) 如图，直线a∥b，正方形ABCD的顶点A、B分别在直线a、b上．若∠2＝73°，则∠1＝．

答案解析收藏纠错 + 选题
12. (2022·威海模拟) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023九上·城关期末) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有实数根，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
14. (2022·威海模拟) 一组数据1、3、 $\text{[math]}$ 、4、5的平均数是5，这组数据的中位数是．

答案解析收藏纠错 + 选题
15. (2024九下·凉州模拟) 设 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则x的值是.

答案解析收藏纠错 + 选题
16. (2023七上·禹城月考) 算式 $\text{[math]}$ 按照性质符号读作为：．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·威海模拟) 解不等式组 $\text{[math]}$ 并写出该不等式组的整数解．

答案解析收藏纠错 + 选题
18. (2022·威海模拟) 激光电视的光源是激光，它运用反射成像原理，屏幕不通电无辐射，降低了对消费者眼睛的伤害．根据THX观影标准，当观影水平视场角“ $\text{[math]}$ ”的度数处于 $\text{[math]}$ 到 $\text{[math]}$ 之间时（如图1），双眼肌肉处于放松状态，是最佳的感官体验的观影位．
1. （1）小丽家决定要买一个激光电视，她家客厅的观影距离（人坐在沙发上眼睛到屏幕的距离）为3.5米，小佳家要选择电视屏幕宽（图2中的BC的长）在什么范围内的激光电视就能享受黄金观看体验？（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
2. （2）由于技术革新和成本降低，激光电视的价格逐渐下降，某电器商行经营的某款激光电视今年每台销售价比去年降低4000元，在销售量相同的情况下，今年销售额在去年销售总额100万元的基础上减少 $\text{[math]}$ ，今年这款激光电视每台的售价是多少元？
答案解析收藏纠错 + 选题
19. (2022·威海模拟) 某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．
1. （1）根据图示填写下表：
  
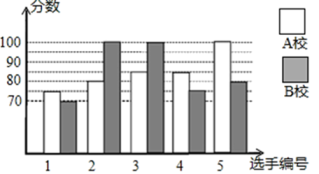
  平均数/分
  
  中位数/分
  
  众数/分
  
  A校
  
  85
  
  B校
  
  85
  
  100
2. （2）结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；
3. （3）计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．
答案解析收藏纠错 + 选题
20. (2022·威海模拟) 如图，四边形ABCD内接于⊙O，∠BAD＝90°，AD、BC的延长线交于点F，点E在CF上，且∠DEC＝∠BAC．
1. （1）求证：DE是⊙O的切线；
2. （2）当AB＝AC时，若CE＝4，EF＝6，求⊙O的半径．
答案解析收藏纠错 + 选题
21. (2022·威海模拟) 我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销．经过调查，得到如表数据：
销售单价x（元/件）
…
30
40
50
60
…
每天销售量y（件）
…
500
400
300
200
…
1. （1）上表中x、y的各组对应值满足一次函数关系，请求出y与x的函数关系式；
2. （2）物价部门规定，该工艺品销售单价最高不能超过45元/件：
  ①销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
  ②该工艺厂积极投入到慈善事业，它将该工艺品每件销售利润中抽取2元捐赠给我市的公共卫生事业，并且捐款后每天的利润不低于7600元，则工艺厂每天从这件工艺品的利润中最多可捐出多少元？
答案解析收藏纠错 + 选题
22. (2022·威海模拟) 在如图的网格中建立平面直角坐标系， $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，格点 $\text{[math]}$ ，只用无刻度的直尺在网格中完成下列画图，画图结果用实线表示，过程用虚线表示，并回答问题．
⑴作 $\text{[math]}$ 的中线 $\text{[math]}$ ；
⑵在 $\text{[math]}$ 上找一点 $\text{[math]}$ ，使得 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ；
⑶作点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点 $\text{[math]}$ ；
⑷线段 $\text{[math]}$ 和线段 $\text{[math]}$ 存在一种特殊关系，即其中一条线段沿某条直线对折可以得到另一条线段，直接写出这条直线的解析式．

答案解析收藏纠错 + 选题
23. (2022·威海模拟) 如图，在平面直角坐标系中，已知两点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在第一象限， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．
1. （1）点 $\text{[math]}$ 的坐标为：（用含 $\text{[math]}$ ， $\text{[math]}$ 的式子表示）；
2. （2）求证： $\text{[math]}$ ；
3. （3）设点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，求证： $\text{[math]}$ ， $\text{[math]}$ 关于 $\text{[math]}$ 轴对称．
答案解析收藏纠错 + 选题
24. (2022·威海模拟) 如图，抛物线y=kx²-2kx-3k交x轴于A、B两点，交y轴于点C，已知OC=OB．
1. （1）求抛物线解析式；
2. （2）在直线BC上求点P，使PA+PO的值最小；
3. （3）抛物线上是否存在点Q，使△QBC的面积等于6？若存在，请求出Q的坐标；若不存在请说明理由．
答案解析收藏纠错 + 选题