题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

江苏省苏州市2023年九年级数学一模模拟试题

更新时间：2023-04-22 浏览次数：132 类型：中考模拟

一、单选题

1. (2024九下·长沙模拟) $\text{[math]}$ 的倒数是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·苏州模拟) 某种细菌细胞整的厚度为0.00000015m，数字0.00000015用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·苏州模拟) 如图，该几何体是由5个相同的小正方体搭成的，则这个几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·苏州模拟) 如图，已知 $\text{[math]}$ 是圆O的直径，点C，D在圆O上，且 $\text{[math]}$ ，则 $\text{[math]}$ 度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·苏州模拟) 某初中男子篮球队队员的身高数据是：180，175，187，186，184.这组数据的中位数是（）

A . 187 B . 184 C . 183 D . 180

答案解析收藏纠错 + 选题
6. (2023·苏州模拟) 上海与北京之间的铁路距离约为1400km，乘坐高铁列车比乘坐普通列车能提前4h到达.已知高铁列车的平均行驶速度是普通快车的2倍，设普通快车的平均行驶速度为xkm/h，根据题意所列出的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·苏州模拟) 已知关于x的一元二次方程 $\text{[math]}$ （m，h，k均为常数且 $\text{[math]}$ ）的解是 $\text{[math]}$ ， $\text{[math]}$ ，则关于x的一元二次方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·苏州模拟) 如图，在矩形 $\text{[math]}$ 中，动点M从点A出发沿边 $\text{[math]}$ 向点D匀速运动，动点N从点B出发沿边 $\text{[math]}$ 向点C匀速运动，连接 $\text{[math]}$ .动点M，N同时出发，点M运动的速度为每秒1个单位长度，点N运动的速度为每秒3个单位长度.当点N到达点C时，M，N两点同时停止运动.在运动过程中，将四边形 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，得到四边形 $\text{[math]}$ .若在某一时刻，点B的对应点 $\text{[math]}$ 恰好与点D重合，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·渝北开学考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2024八下·福州期中) 函数 $\text{[math]}$ 中自变量x的取值范围是．

答案解析收藏纠错 + 选题
11. (2023·苏州模拟) 二次函数 $\text{[math]}$ 的顶点坐标为.

答案解析收藏纠错 + 选题
12. (2023·苏州模拟) 不透明的袋子中装有2个红球、3个黑球，这些球除颜色外无其他差别.从袋子中随机摸出一个球，则摸出红球的概率是.

答案解析收藏纠错 + 选题
13. (2023·苏州模拟) 如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y= $\text{[math]}$ 的图象上，则k的值为.

答案解析收藏纠错 + 选题
14. (2024九下·相城月考) 若一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是。

答案解析收藏纠错 + 选题
15. (2023·苏州模拟) 在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ 其中 $\text{[math]}$ 为实数）.当 $\text{[math]}$ 的长最小时， $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
16. (2023·苏州模拟) 如图，点A的坐标为 $\text{[math]}$ ，点B是x轴正半轴上的一点，将线段 $\text{[math]}$ 绕点A按逆时针方向旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ .若点C的坐标为 $\text{[math]}$ ，则m的值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2023·苏州模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023·苏州模拟) 解不等式组： $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2023·苏州模拟) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2023·苏州模拟) 如图，已知AB=CD，AB∥CD，E、F是AC上两点，且AF=CE．
1. （1）说明：△ABE≌△CDF；
2. （2）连接BC，若∠CFD=100°，∠BCE=30°，求∠CBE的度数．
答案解析收藏纠错 + 选题
21. (2023·苏州模拟) 某校在举行运动会时成立了志愿者服务队，设立四个服务监督岗： $\text{[math]}$ .安全监督岗； $\text{[math]}$ .卫生监督岗； $\text{[math]}$ .文明监督岗； $\text{[math]}$ .检录服务岗.小明和小丽报名参加了志愿者服务工作，学校将报名的志愿者随机分配到四个监督岗.
1. （1）小明被分配到文明监督岗的概率为；
2. （2）用列表法或画树状图法，求小明和小丽被分配到同一个服务监督岗的概率.
答案解析收藏纠错 + 选题
22. (2023·苏州模拟) 为了解学生的科技知识情况，某校在七，八年学生中举行了科技知识竞赛（七，八年各有300名学生）.现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：
收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77.
八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41.
整理数据：

$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
七年级
0
1
0
11
7
1
八年级
1
0
0
7
a
2
分析数据：

平均数
众数
中位数
七年级
78
75
b
八年级
78
81
80.5
应用数据：
1. （1）由上表填空： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）估计该校七、八两个年级在本次竞赛中成绩在90分以上（含90分）的学生共有多少人？
3. （3）你认为哪个年级的学生科技知识的总体水平较好，请说明理由.
答案解析收藏纠错 + 选题
23. (2023·苏州模拟) 如图，垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处（点A、B、C在同一直线上），某测量员从悬崖底C点出发沿水平方向前行60米到D点，再沿斜坡DE方向前行65米到E点（点A、B、C、D、E在同一平面内），在点E处测得5G信号塔顶端A的仰角为37°，悬崖BC的高为92米，斜坡DE的坡度 $\text{[math]}$ .（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）求斜坡DE的高EH的长；
2. （2）求信号塔AB的高度.
答案解析收藏纠错 + 选题
24. (2023九上·义乌月考) 为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y千克与每平方米种植的株数x（ $\text{[math]}$ ，且x为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．
1. （1）求y关于x的函数表达式．
2. （2）每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？
答案解析收藏纠错 + 选题
25. (2023·苏州模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 直径，E，C是 $\text{[math]}$ 上的两点， $\text{[math]}$ 是 $\text{[math]}$ 的切线， $\text{[math]}$ 于点D， $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点G.
1. （1） ①若 $\text{[math]}$ ， $\text{[math]}$ ，求直径 $\text{[math]}$ 的长；
  ②探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三者之间的数量关系.
2. （2）若 $\text{[math]}$ ，当点C在半圆上运动时，问四边形 $\text{[math]}$ 的面积是否存在最大值？如果存在，求出最大值；如果不存在，请说明理由.
答案解析收藏纠错 + 选题
26. (2023·苏州模拟) 在平面直角坐标系xOy中，已知抛物线 $\text{[math]}$ 经过A（4，0），B（1，4）两点.P是抛物线上一点，且在直线AB的上方.
1. （1）求抛物线的解析式；
2. （2）若△OAB面积是△PAB面积的2倍，求点P的坐标；
3. （3）如图，OP交AB于点C， $\text{[math]}$ 交AB于点D.记△CDP，△CPB，△CBO的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .判断 $\text{[math]}$ 是否存在最大值.若存在，求出最大值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
27. (2023·苏州模拟) 【教材再现】
在初中数学教材中有这样一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例.如图1，直线 $\text{[math]}$ ，直线m和直线n分别与直线 $\text{[math]}$ 和直线 $\text{[math]}$ 相交于点A，点B，点F，点D，直线m和直线n相交于点E，则 $\text{[math]}$ ；
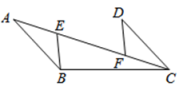
【探究发现】
如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D在边 $\text{[math]}$ 上（不与点B，点C重合），连接 $\text{[math]}$ ，点E在边 $\text{[math]}$ 上， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的长；
3. （3）点H在射线AC上，连接EH交线段 $\text{[math]}$ 于点G，当 $\text{[math]}$ ，且 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

试卷信息