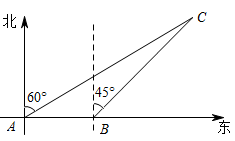四川省内江市市中区全安中学2023年中考数学一模试卷

更新时间：2024-07-29 浏览次数：55 类型：中考模拟

一、选择题（本大题共12小题，每小题3分，共36分。）

1. (2023·内江模拟) - $\text{[math]}$ 的绝对值是（）

A . - $\text{[math]}$ B . -2 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2023九下·市中区模拟) 可燃冰学名叫“天然气水合物”，是一种高效清洁储量巨大的新能源，据报道，仅我国可燃冰预测远景资源量就超过了1000亿吨油当量.将1000亿用科学记数法可表示为（）

A . 1×10¹¹吨 B . 1000×10⁸吨 C . 10×10¹⁰吨 D . 1×10³吨

答案解析收藏纠错 + 选题
3. (2023·内江模拟) 下列几何体中，主视图是矩形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·内江模拟) 下列事件中是必然事件的是（）

A . 投掷一枚质地均匀的硬币100次，正面朝上的次数为50次 B . 任意一个六边形的外角和等于720° C . 同时掷两枚质地均匀的骰子，两个骰子的点数相同 D . 367个同学参加一个集会，他们中至少有两个同学的生日是同月同日

答案解析收藏纠错 + 选题
5. (2023·内江模拟) 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023·内江模拟) 下列各式正确的是（）

A . a⁴•a⁵＝a²⁰ B . a²+2a³＝2a⁵ C . a⁴÷a＝a³ D . （-a²b³）²＝a⁴b⁹

答案解析收藏纠错 + 选题
7. (2023·内江模拟) 函数y＝ $\text{[math]}$ 的自变量的取值范围是（）

A . x≥-1 B . x≥-1且x≠0 C . x＞0 D . x＞-1且x≠0

答案解析收藏纠错 + 选题
8. (2023·内江模拟) 一个等腰三角形的底边长是5，腰长是一元二次方程x²﹣6x+8＝0的一个根，则此三角形的周长是（）

A . 12 B . 13 C . 14 D . 12或14

答案解析收藏纠错 + 选题
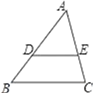
9. (2023·内江模拟) 如图，在△ABC中，DE∥BC，AD＝6，DB＝3，AE＝4，则AC的长为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
10. (2022九上·丰城开学考) 如图，四边形ABCD内接于⊙O，连接OB，OD，BD，若∠C＝110°，则∠OBD＝（）

A . 15° B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题
11. (2023·内江模拟) 若关于x的不等式组 $\text{[math]}$ 恰有三个整数解，则实数a的取值范围是（）

A . 4＜a≤5 B . 8＜a≤10 C . 8≤a＜10 D . a≤8或a＞10

答案解析收藏纠错 + 选题
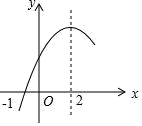
12. (2023九上·海曙月考) 二次函数y＝ax²+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：（1）abc＜0；（2）4a+c＞2b；（3）3b﹣2c＞0；（4）若点A（﹣2，y₁）、点B（﹣ $\text{[math]}$ ， y₂）、点C（ $\text{[math]}$ ， y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）4a+2b≥m（am+b）（m为常数）.其中正确的结论有（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，每小题5分，共20分）

13. (2023·内江模拟) 分解因式：3x²-12xy+12y²＝．

答案解析收藏纠错 + 选题
14. (2023九下·市中区模拟) 现有五张正面图形分别是平行四边形、圆、等边三角形、正五边形、菱形的卡片，它们除正面图形不同，其它完全相同．将它们背面朝上洗匀后，从中随机抽取一张卡片，卡片的正面图形既是中心对称图形又是轴对称图形的概率是．

答案解析收藏纠错 + 选题
15. (2023九下·市中区模拟) 已知2x+y＝10xy，则代数式 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
16. (2022九上·双流期中) 如图，在以O为原点的直角坐标系中，点A，C分别在x轴、y轴的正半轴上，点B在第一象限内，四边形OABC是矩形，反比例函数y＝ $\text{[math]}$ （x＞0）与AB相交于点D，与BC相交于点E，若BE＝4CE，四边形ODBE的面积是8，则k＝.

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，共44分。）

17. (2023九下·市中区模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
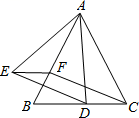
18. (2023八下·长安期末) 如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB＝60°，DC＝EF.
1. （1）求证：四边形EFCD是平行四边形；
2. （2）若BF＝EF，求证：AE＝AD.
答案解析收藏纠错 + 选题
19. (2023·内江模拟) 为了贯彻“减负增效”精神，某校掌握2022～2023学年度九年级600名学生每天的自主学习情况，某校学生会随机抽查了2022～2023学年度九年级的部分学生，并调查他们每天自主学习的时间.根据调查结果，制作了两幅不完整的统计图（图1，图2），请根据统计图中的信息回答下列问题：
1. （1）本次调查的学生人数有人；
2. （2）图2中α是 ▲ 度，并将图1补充完整；
3. （3）请估算该校2022～2023学年度九年级学生自主学习时间不少于1.5小时的有人；
4. （4）老师想从学习效果较好的4位同学（分别记为A、B、C、D，其中A为小亮）中随机选择两位进行学习经验交流，用列表法或画树状图的方法求出选中小亮的概率.
答案解析收藏纠错 + 选题
20. (2023·恩施模拟) 如图，一艘轮船从点 $\text{[math]}$ 处以 $\text{[math]}$ 的速度向正东方向航行，在 $\text{[math]}$ 处测得灯塔 $\text{[math]}$ 在北偏东 $\text{[math]}$ 方向上，继续航行 $\text{[math]}$ 到达 $\text{[math]}$ 处，这时测得灯塔 $\text{[math]}$ 在北偏东 $\text{[math]}$ 方向上，已知在灯塔 $\text{[math]}$ 的四周 $\text{[math]}$ 内有暗礁，问这艘轮船继续向正东方向航行是否安全？并说明理由.（提示： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
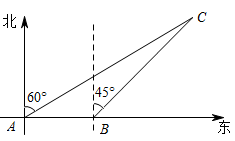
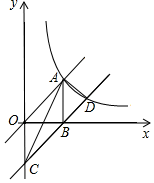
21. (2023·内江模拟) 如图，正比例函数y₁＝kx与反比例函数y＝ $\text{[math]}$ （x＞0）交于点A（2，3），AB⊥x轴于点B，平移直线y₁＝kx使其经过点B，得到直线y₂ ， y₂与y轴交于点C，与y＝ $\text{[math]}$ 交于点D.
1. （1）求正比例函数y₁＝kx及反比例函数y＝ $\text{[math]}$ 的解析式；
2. （2）求点D的坐标；
3. （3）求△ACD的面积.
答案解析收藏纠错 + 选题

四、填空题（本大题共4小题，每小题6分，共24分）

22. (2023·内江模拟) 已知b＝ $\text{[math]}$ -1，则a^b＝.

答案解析收藏纠错 + 选题
23. (2023·内江模拟) 如图，点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第2023次运动后动点P的坐标是 .

答案解析收藏纠错 + 选题
24. (2023·内江模拟) 已知x，y，z为实数，满足 $\text{[math]}$ ，那么x²+y²+z²的最小值是

答案解析收藏纠错 + 选题
25. (2023·内江模拟) 如图，在菱形ABCD中，tanA＝ $\text{[math]}$ ， M，N分别在边AD，BC上，将四边形AMNB沿MN翻折，使AB的对应线段EF经过顶点D，延长NF交DC于点H，当EF⊥AD时， $\text{[math]}$ 的值为 .

答案解析收藏纠错 + 选题

五、解答题（本大题共3小题，每小题12分，共36分）

26. (2023·内江模拟) 某电器城经销A型号彩电，今年四月份每台彩电售价与去年同期相比降价500元，结果卖出彩电的数量相同，但去年销售额为5万元，今年销售额为4万元.
1. （1）问去年四月份每台A型号彩电售价是多少元？
2. （2）为了改善经营，电器城决定再经销B型号彩电.已知A型号彩电每台进货价为1800元，B型号彩电每台进货价为1500元，电器城预计用不多于3.3万元且不少于3.2万元的资金购进这两种彩电共20台，问有哪几种进货方案？
3. （3）电器城准备把A型号彩电继续以原价出售，B型号彩电以每台1800元的价格出售，在这批彩电全部卖出的前提下，如何进货才能使电器城获利最大？最大利润是多少？
答案解析收藏纠错 + 选题
27. (2023·内江模拟) 如图，PA为⊙O的切线，A为切点，直线PO交⊙O于点E，F过点A作PO的垂线AB垂足为D，交⊙O于点B，延长BO与⊙O交于点C，连接AC，BF.
1. （1）求证：PB与⊙O相切；
2. （2）是探究线段EF，OD，OP之间的数量关系，并加以证明；
3. （3）若tan∠F＝ $\text{[math]}$ ，求cos∠ACB的值.
答案解析收藏纠错 + 选题
28. (2023·内江模拟) 如图，二次函数y＝-x²+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB＝OC，点D在函数图象上，CD∥x轴且CD＝2，直线l是抛物线的对称轴，E是抛物线的顶点.
1. （1）求b、c的值；
2. （2）如图1，连BE，线段OC上的点F关于直线l的对称点F′恰好在线段BE上，求点F的坐标；
3. （3）如图2，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？若存在，求出点Q的坐标；若不存在，说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

四川省内江市市中区全安中学2023年中考数学一模试卷

副标题：

*注意事项：

四川省内江市市中区全安中学2023年中考数学一模试卷

试题分析

总体分析

题量分析

难度分析

知识点分析