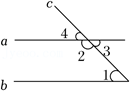

①若∠1=∠3,则 AD∥BC;
②若 AD∥BC,则∠1=∠2=∠3;
③若∠1=∠3,AD∥BC,则∠1=∠2;
④若∠C+∠3+∠4=180°,则 AD∥BC.




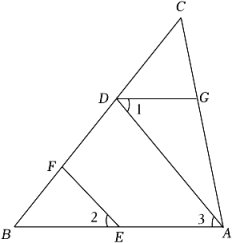
解:∵EF∥AD,(已知)
∴∠2=▲ .( )
∵∠DGA+∠BAC=180°,( )
∴DG∥AB,( )
∴∠1=∠3,( )
∴∠1=∠2.( )

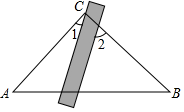
求证: .
证明:∵ 于点A ,
于点F , (已知)
∴ . (垂直的定义)
∴ , ( )
∴▲ ( )
∵ ,(已知)
∴ ▲ . (两直线平行,同位角相等)
∵ ,
∴ . (等量代换)
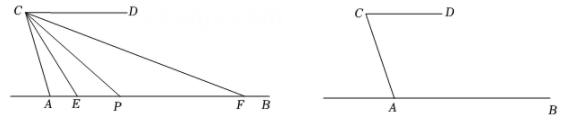
①若∠ACP=36°,则此时CP是否平分∠ECF,请说明理由.
②求∠ECF的度数.

请帮助小亮完成下面的证明:
由题意得∠ABC=90°,∠1=30°,∠2=60°,过点B作 ,
又∵∠2=60°(已知),∴▲ =∠2=60°( ).
∵∠ABC=90°(已知),∴∠CBD= ▲ °.
又∵∠1=30°(已知),∴∠CBD=∠1(等量代换),
∴▲ ▲ (内错角相等,两直线平行).
∵ ,∴
( ).
