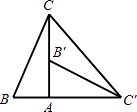

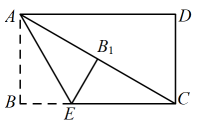

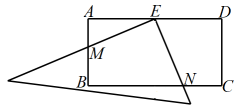
①画出 关于原点
的中心对称图形
;
②画出将 绕点
顺时针旋转90°得到
;
|
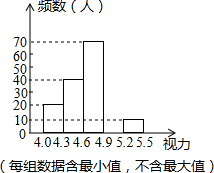
视力 |
频数(人) |
频率 |
|
| 20 | 0.1 |
| | 40 | 0.2 |
| | 70 | 0.35 |
| | | 0.3 |
| | 10 | |
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 |
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S | 1 |
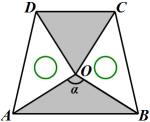
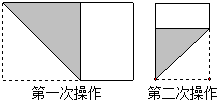
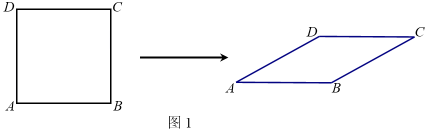
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,;当α=135°时,
.由上表可以得到
( °);
( °),…,由此可以归纳出
=S().