陕西省铜川市2023届高三理数二模试卷

更新时间：2023-05-22 浏览次数：53 类型：高考模拟

一、单选题

1. (2023·铜川模拟) 若全集 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）.

A . {2} B . {3} C . {4} D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·铜川模拟) 已知复数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
3. (2023·铜川模拟) 执行下面的程序框图，则输出S的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·铜川模拟) 如图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC．△ABC的三边所围成的区域记为I，黑色部分记为II，其余部分记为III．在整个图形中随机取一点，此点取自I，II，III的概率分别记为p₁ ， p₂ ， p₃ ，则

A . p₁=p₂ B . p₁=p₃ C . p₂=p₃ D . p₁=p₂+p₃

答案解析收藏纠错 + 选题
5. (2023·铜川模拟) 命题：“ $\text{[math]}$ ， $\text{[math]}$ ”的否定是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·铜川模拟) 已知 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·铜川模拟) 现有甲、乙两组数据，每组数据均由六个数组成，其中甲组数据的平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ，乙组数据的平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ．若将这两组数据混合成一组，则新的一组数据的方差为（）

A . 3.5 B . 4 C . 4.5 D . 5

答案解析收藏纠错 + 选题
8. (2023·铜川模拟) 等比数列 $\text{[math]}$ 满足 $\text{[math]}$ ，设数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，则 $\text{[math]}$ =（）

A . -11 B . -8 C . 5 D . 11

答案解析收藏纠错 + 选题
9. (2023·铜川模拟) 如图，在 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 上分别取点 $\text{[math]}$ 、 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
10. (2023·铜川模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ 分别是双曲线 $\text{[math]}$ 的左、右焦点，直线l经过 $\text{[math]}$ 且与C左支交于P，Q两点，P在以 $\text{[math]}$ 为直径的圆上， $\text{[math]}$ ，则C的离心率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023·铜川模拟) 已知函数 $\text{[math]}$ $\text{[math]}$ 在一个周期内的函数图象如图所示．若方程 $\text{[math]}$ 在区间 $\text{[math]}$ 有两个不同的实数解 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023·铜川模拟) 在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 为菱形， $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为线段 $\text{[math]}$ 的中点， $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点，则下列结论错误的是（）

A . 平面 $\text{[math]}$ 平面 $\text{[math]}$ B . 三棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ C . $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的最小值为 $\text{[math]}$ D . $\text{[math]}$ 与 $\text{[math]}$ 所成角的余弦值为 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2023·铜川模拟) 将四大名著各分一本给甲、乙、丙、丁四人就读，A、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四位旁观者预测分配结果，A说：“甲读《西游记》，乙读《红楼梦》”； $\text{[math]}$ 说：“甲读《水浒传》，丙读《三国演义》”； $\text{[math]}$ 说：“乙读《水浒传》，丙读《西游记》”； $\text{[math]}$ 说：“乙读《西游记》，丁读《三国演义》”.若已知四位旁观者每人预测的两句话中，都是有且只有一句是真的，则可推断丁读的名著是.

答案解析收藏纠错 + 选题
14. (2023·铜川模拟) 已知函数 $\text{[math]}$ ，若 $\text{[math]}$ ，则函数 $\text{[math]}$ 的值域为.

答案解析收藏纠错 + 选题
15. (2023·铜川模拟) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，且点 $\text{[math]}$ 总在直线 $\text{[math]}$ 上，则数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2023·铜川模拟) 已知椭圆 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 与椭圆 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点（其中点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），记 $\text{[math]}$ 面积为 $\text{[math]}$ ，则下列四个结论正确的是.
① $\text{[math]}$ ② $\text{[math]}$ 时， $\text{[math]}$
③ $\text{[math]}$ 的最大值为 $\text{[math]}$ ④当 $\text{[math]}$ 时，点 $\text{[math]}$ 的横坐标为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

17. (2023·铜川模拟) 在 $\text{[math]}$ 中，角 $\text{[math]}$ 所对的边分别为 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，当角 $\text{[math]}$ 取得最大值时，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
18. (2023·铜川模拟) 如图，在斜三棱柱 $\text{[math]}$ 中，底面ABC是边长为2的正三角形， $\text{[math]}$ ，侧棱AD与底面ABC所成角为60°．
1. （1）求证：四边形BCFE为矩形；
2. （2）求平面DBC与平面BCFE夹角的余弦值．
答案解析收藏纠错 + 选题
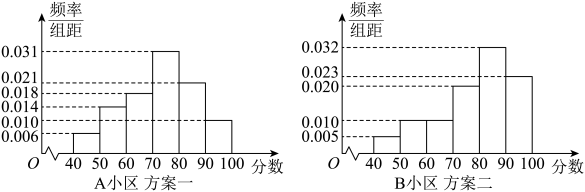
19. (2023·铜川模拟) 为进一步巩固提升全国文明城市，加速推行垃圾分类制度，铜川市推出了两套方案，并分别在 $\text{[math]}$ 、 $\text{[math]}$ 两个大型居民小区内试行.方案一：进行广泛的宣传活动，向小区居民和社会各界宣传垃圾分类的意义，讲解分类垃圾桶的使用方式，垃圾投放时间等，定期召开垃圾分类会议和知识宣传教育活动；方案二：在小区内设立智能化分类垃圾桶，智能垃圾桶操作简单，居民可以通过手机进行自动登录、称重、积分等一系列操作.并建立激励机制，比如，垃圾分类换积分兑换礼品等，以激发带动居民参与垃圾分类的热情.经过一段时间试行之后，在这两个小区内各随机抽取了100名居民进行问卷调查，记录他们对试行方案的满意度得分（满分100分），将数据分成6组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，并整理得到如图所示的频率分布直方图：
1. （1）请通过频率分布直方图分别估计两种方案满意度的平均得分，判断哪种方案的垃圾分类推广措施更受居民欢迎（同一组中的数据用该组中间的中点值作代表）；
2. （2）以样本频率估计概率，若满意度得分不低于70分认为居民赞成推行此方案，低于70分认为居民不赞成推行此方案，规定小区居民赞成率不低于 $\text{[math]}$ 才可在该小区继续推行该方案，判断两小区哪个小区可继续推行方案？
3. （3）根据（2）中结果，从可继续推行方案的小区内随机抽取5个人，用 $\text{[math]}$ 表示赞成该小区推行方案的人数，求 $\text{[math]}$ 的分布列及数学期望.
答案解析收藏纠错 + 选题
20. (2023·铜川模拟) 已知点F为抛物线E： $\text{[math]}$ （ $\text{[math]}$ ）的焦点，点P（−3，2）， $\text{[math]}$ ，若过点P作直线与抛物线E顺次交于A，B两点，过点A作斜率为1的直线与抛物线的另一个交点为点C．
1. （1）求抛物线E的标准方程；
2. （2）求证：直线BC过定点；
3. （3）若直线BC所过定点为点Q，△QAB，△PBC的面积分别为S₁ ， S₂ ，求 $\text{[math]}$ 的取值范围
答案解析收藏纠错 + 选题
21. (2023·铜川模拟) 已知函数 $\text{[math]}$ ．
1. （1）若函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极值，求 $\text{[math]}$ 的值及函数的单调区间；
2. （2）若函数 $\text{[math]}$ 有两个零点，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
22. (2023·铜川模拟) 在直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 为参数），以坐标原点 $\text{[math]}$ 为极点， $\text{[math]}$ 轴的正半轴为极轴建立极坐标系，曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ， $\text{[math]}$ 为曲线 $\text{[math]}$ 上一点.
1. （1）求 $\text{[math]}$ 到直线 $\text{[math]}$ 距离的最大值；
2. （2）若 $\text{[math]}$ 为直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 第一象限的交点，且 $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
23. (2023·铜川模拟) 设函数 $\text{[math]}$ ．
1. （1）解不等式 $\text{[math]}$ ；
2. （2）令 $\text{[math]}$ 的最小值为T，正数 $\text{[math]}$ 满足 $\text{[math]}$ ，证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题