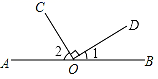



已知:如图,BC∥DE,BE、DF分别是∠ABC、∠ADE的平分线.
求证:∠1=∠2.
证明:∵BC∥DE,
∴∠ABC=∠ADE( ).
∵BE、DF分别是∠ABC、∠ADE的平分线.
∴∠3=∠ABC,∠4=
∠ADE.
∴∠3=∠4.
∴ ▲ ∥ ▲ ( ).
∴∠1=∠2( ).


请根据以上信息解答下列问题:
阅读理解:
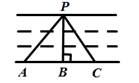
如图1,已知点A是BC外一点,连接AB、AC.求∠BAC+∠B+∠C的度数.
解:过点A作DEBC.
∵DEBC,
∴∠B=∠EAB,∠C=∠DAC.
又∵∠EAB+∠BAC+∠DAC=180°,
∴∠BAC+∠B+∠C=180°.

如图2,已知ABDE,试说明:∠D+∠BCD-∠B=180°.(提示:过点C作CF
AB)

如图3,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1=度.

①如图4,若ABDE,∠B、∠C、∠D有怎样的关系:;
②如图5,若ABDE,∠B、∠C、∠D有怎样的关系:.