山西省晋中市平遥县2022-2023学年八年级下学期数学期中...

经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低1380吨，该企业有哪些购买方案呢？这解决这个问题，高购买A型污水处理设备x台，所列不等式组正确的是　　

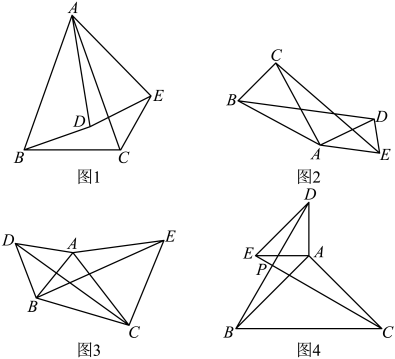
问题：如图，在中， ， 点D在边上（不与点A，点B重合），点E在边上（不与点A，点C重合），连接 ， ， 与相交于点F．若        ，求证： ．

学习了一元一次不等式组的解法，老师给同学们布置了一个任务，请大家探究并求出不等式 的解集．

小丽类比有理数的乘法法则，根据“同号两数相乘，积为正”可以得到：①或② ， 解不等式组①得 ， 解不等式组②得 ， 所以原不等式解集为或 ． 请你仿照上述方法，求不等式的的解集．

已知：如图， ，点A，B分别在射线OM，ON上，且满足 ．

求作：线段OB上的一点C，使 的周长等于线段 的长．

以下是小宇分析和求解的过程，请补充完整：首先画草图进行分析，如图1所示，若符合题意得点C已经找到，即 得周长等于OB的长，那么由 ，可以得到 ．

对于这个式子，可以考虑用截长得办法，在BC上取一点D，使得 ，那么就可以得到 ．

若连接AD，由．（填推理依据）．可知点C在线段AD得垂直平分线上，于是问题得解法就找到了．

请根据小宇得分析，在图2中完成作图（尺规作图，不写做法，保留作图痕迹）．

在学习全等三角形的知识时，数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成的，在相对位置变化的同时，始终存在一对全等三角形．兴趣小组成员经过研讨给出定义：如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，则称此图形为“手拉手全等模型”．因为顶点相连的四条边，可以形象地看作两双手，所以通常称为“手拉手模型”．如图1，与都是等腰三角形，其中 ， 则 ．