 B .
B .  C .
C . 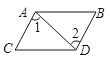 D .
D . 
|
支撑物高 |
10 |
20 |
30 |
40 |
50 |
… |
|
下滑时间 |
3.25 |
3.01 |
2.81 |
2.66 |
2.56 |
… |
以下结论错误的是( )
 B .
B .  C .
C .  D .
D . 
①在同一平面内,两边分别平行的两角相等;②两条直线被第三条直线所截,内错角相等;③三角形的三条高线所在直线交于一点;④如果 , 那么
;⑤过一点有且只有一条直线与已知直线平行


①小长方形的较长边为;
②阴影A的较短边和阴影B的较短边之和为;
③若x为定值,则阴影A和阴影B的周长和为定值;
④当时,阴影A和阴影B的面积和为定值.


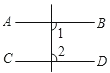
已知:如图,与
互补,
, 求证:
.

证明:∵与
互补,即 ▲ ,
∴//
( ).
∴( ).
又∵ , (已知).
∴ , 即
. ( ).
∴ ▲ // ▲ ( ).
∴ . ( ).


|
三角形数 古希腊著名数学家的毕达哥拉斯学派把1,3,6,10,...,这样的数称为“三角形数”,第n个“三角形数”可表示为: |
发现:每相邻两个“三角形数”的和有一定的规律.如:;
;
;…
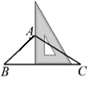
①若恰好平分
, 则
;
②若在
内部,请直接写出
与
有怎样的数量关系;
