吉林省梅河口市2023届高三下学期6月第七次数学模拟考试试卷

更新时间：2023-08-22 浏览次数：51 类型：高考模拟

一、单选题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的，请仔细审题，认真做答

1. (2023高三下·梅河口月考) 若复数 $\text{[math]}$ 满足 $\text{[math]}$ ，其中 $\text{[math]}$ 为虚数单位，则 $\text{[math]}$ （）

A . 0 B . -1 C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
2. (2023高三下·梅河口月考) 已知集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高三下·梅河口月考) 设非零向量 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 在 $\text{[math]}$ 上的投影向量为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高三下·梅河口月考) 从2至8的7个整数中随机取2个不同的数，若取出的2个数互质，则取出两个数都是奇数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高三下·梅河口月考) 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ 两点， $\text{[math]}$ 是该双曲线的焦点，且满足 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
6. (2023高三下·梅河口月考) 若球 $\text{[math]}$ 是正三棱锥 $\text{[math]}$ 的外接球， $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ ，过点 $\text{[math]}$ 作球 $\text{[math]}$ 的截面，则所得的截面中面积最小的截面的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高三下·梅河口月考) 若函数 $\text{[math]}$ 有两个极值点 $\text{[math]}$ ，且 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三下·梅河口月考) 已知 $\text{[math]}$ 则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多个选项是等合题目要求的，全部选对的得5分，有选错的得0分，部分选对的得2分，请仔细审题，认真皕答

9. (2023高三下·梅河口月考) 十六世纪中叶，英国数学家雷科德在《励智石》一书中首先把“=”作为等号使用，后来英国数学家哈里奥特首次使用“<”和“>”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远.若 $\text{[math]}$ ，则下列说法不成立的是（）

A . 若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高三下·梅河口月考) 若函数 $\text{[math]}$ 同时满足以下条件：① $\text{[math]}$ 是函数 $\text{[math]}$ 的零点，且 $\text{[math]}$ ；② $\text{[math]}$ ，有 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . 将 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ 个单位长度得到的图象解析式为 $\text{[math]}$ C . $\text{[math]}$ 在 $\text{[math]}$ 上单调递减 D . 直线 $\text{[math]}$ 是曲线 $\text{[math]}$ 的一条对称轴

答案解析收藏纠错 + 选题
11. (2023高三下·梅河口月考) 已知点 $\text{[math]}$ 是抛物线 $\text{[math]}$ 的焦点， $\text{[math]}$ 为坐标原点，直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ 两点，抛物线 $\text{[math]}$ 的准线与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，下列说法正确的是（）

A . 若 $\text{[math]}$ 过抛物线 $\text{[math]}$ 的焦点 $\text{[math]}$ ，则直线 $\text{[math]}$ 斜率之积为定值 B . 若抛物线上的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离为4，则抛物线的方程为 $\text{[math]}$ C . 以 $\text{[math]}$ 为直径的圆与准线相切 D . 直线 $\text{[math]}$ 过点 $\text{[math]}$ 且交 $\text{[math]}$ 于不同的 $\text{[math]}$ 两点，则 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高三下·梅河口月考) 已知正方体 $\text{[math]}$ 的棱长为 $\text{[math]}$ 为空间中任一点，则下列结论中正确的是（）

A . 若 $\text{[math]}$ 为线段 $\text{[math]}$ 上任一点，则 $\text{[math]}$ 与 $\text{[math]}$ 所成角的余弦值范围为 $\text{[math]}$ B . 若 $\text{[math]}$ 为正方形 $\text{[math]}$ 的中心，则三棱锥 $\text{[math]}$ 外接球的体积为 $\text{[math]}$ C . 若 $\text{[math]}$ 在正方形 $\text{[math]}$ 内部，且 $\text{[math]}$ ，则点 $\text{[math]}$ 轨迹的长度为 $\text{[math]}$ D . 若三棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ 恒成立，点 $\text{[math]}$ 轨迹的为圆的一部分

答案解析收藏纠错 + 选题

三、填空题：本大题共4小题，每小题5分，共20分，请仔细审题，认真做答

13. (2023高三下·梅河口月考) $\text{[math]}$ 的展开式中， $\text{[math]}$ 的系数为.

答案解析收藏纠错 + 选题
14. (2023高三下·梅河口月考) 由直线 $\text{[math]}$ 上一点 $\text{[math]}$ 向圆 $\text{[math]}$ 引切线，则切线长的最小值为.

答案解析收藏纠错 + 选题
15. (2023高三下·梅河口月考) 已知函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上存在零点，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题
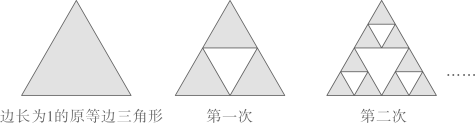
16. (2023高三下·梅河口月考) 如图，将一个边长为1的正三角形分成四个全等的正三角形，第一次挖去中间的一个小三角形，将剩下的三个小正三角形，再分别从中间挖去一个小三角形，保留它们的边，重复操作以上做法，得到的集合为谢尔宾斯基三角形.设 $\text{[math]}$ 是第 $\text{[math]}$ 次挖去的小三角形面积之和（如 $\text{[math]}$ 是第1次挖去的中间小三角形面积， $\text{[math]}$ 是第2次挖去的三个小三角形面积之和），则 $\text{[math]}$ ；若操作 $\text{[math]}$ 次后剩余部分面积不大于原图面积的一半，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题

四、解答题：本大题共6小题，共70分，请仔细审题，认真做答

17. (2023高三下·梅河口月考) 如图所示，在直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折起到 $\text{[math]}$ 的位置，使平面 $\text{[math]}$ 平面 $\text{[math]}$ ，点 $\text{[math]}$ 满足 $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的余弦值.
答案解析收藏纠错 + 选题
18. (2023高三下·梅河口月考) 记 $\text{[math]}$ 的内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，分别以 $\text{[math]}$ 为边长的三个正三角形的面积依次为 $\text{[math]}$ ，已知 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的面积；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2023高三下·梅河口月考) $\text{[math]}$ 为数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和，已知 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式 $\text{[math]}$ ；
2. （2）数列 $\text{[math]}$ 依次为： $\text{[math]}$ ，规律是在 $\text{[math]}$ 和 $\text{[math]}$ 中间插入 $\text{[math]}$ 项，所有插入的项构成以3为首项，3为公比的等比数列，求数列 $\text{[math]}$ 的前100项的和.
答案解析收藏纠错 + 选题
20. (2023高三下·梅河口月考) 某学校离三年级开学之初增加早自习，早饭在校食堂就餐人数增多，为了缓解就餐压力，学校在原有一个餐厅的基础上增加了一个餐厅，分别记做餐厅甲和餐厅乙，经过一周左右统计调研分析：前一天选择餐厅甲就餐第二天选择餐厅甲就餐的概率是 $\text{[math]}$ ，择餐厅乙就餐的概率为 $\text{[math]}$ ，前一天选择餐厅乙就餐第二天选择餐厅乙就餐的概率是 $\text{[math]}$ ，选择餐厅甲就餐的概率也为 $\text{[math]}$ ，如此往复.假设学生第一天选择餐厅甲就餐的概率是 $\text{[math]}$ ，择餐厅乙就餐的概率是 $\text{[math]}$ ，记某同学第 $\text{[math]}$ 天选择甲餐厅就餐的概率为 $\text{[math]}$ .
1. （1）记某班级的3位同学第二天选择餐厅甲的人数为 $\text{[math]}$ ，求 $\text{[math]}$ 的分布列，并求 $\text{[math]}$ ；
2. （2）请写出 $\text{[math]}$ 的通项公式；
答案解析收藏纠错 + 选题
21. (2023高三下·梅河口月考) 已知椭圆 $\text{[math]}$ 的一个顶点为 $\text{[math]}$ ，焦距为 $\text{[math]}$ .椭圆 $\text{[math]}$ 的左､右顶点分别为 $\text{[math]}$ 为椭圆 $\text{[math]}$ 上异于 $\text{[math]}$ 的动点， $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ 与椭圆 $\text{[math]}$ 的另一个交点为 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 的标准方程；
2. （2）直线 $\text{[math]}$ 是否过 $\text{[math]}$ 轴上的定点？若过定点，求出该定点的坐标；若不过定点，说明理由.
答案解析收藏纠错 + 选题
22. (2023高三下·梅河口月考) 已知 $\text{[math]}$ 且 $\text{[math]}$ ，函数 $\text{[math]}$ .
1. （1）讨论 $\text{[math]}$ 的单调区间；
2. （2）若曲线 $\text{[math]}$ 与直线 $\text{[math]}$ 恰有一个交点，求 $\text{[math]}$ 取值范围.
答案解析收藏纠错 + 选题