河南省2023年初中数学学业水平测试

更新时间：2023-07-19 浏览次数：134 类型：中考模拟

一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个正确的。

1. (2023·河南模拟) $\text{[math]}$ 的绝对值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023六上·大庆开学考) 2023全国“两会”政府工作报告中指出：我国粮食产量连年稳定在1.3万亿斤以上.其中数据“1.3万亿”用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·河南模拟) 某几何体的三视图如图所示，这个几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·河南模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·河南模拟) 如图，在 $\text{[math]}$ 中，作边AB的垂直平分线，交边BC于点 $\text{[math]}$ ，连接AD.若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 50° B . 40° C . 35° D . 30°

答案解析收藏纠错 + 选题
6. (2023·河南模拟) 把不等式组 $\text{[math]}$ 的解集表示在数轴上，下列选项正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023·河南模拟) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则 $\text{[math]}$ 的值可以是（）

A . -3 B . -2 C . 0 D . -1

答案解析收藏纠错 + 选题
8. (2023·河南模拟) 近年来我国航天事业取得了一系列的伟大成就，现有5张卡片正面图案如图所示，它们除此之外其他完全相同，把这5张卡片背面朝上洗匀，从中随机抽取两张卡片正面图案恰好是“嫦娥五号”和“卫星导航系统”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·河南模拟) 如图，在平面直角坐标系中，四边形OABC的顶点 $\text{[math]}$ 在原点上，OA边在 $\text{[math]}$ 轴的正半轴上， $\text{[math]}$ 轴， $\text{[math]}$ ，将四边形OABC绕点 $\text{[math]}$ 送时针旋转，每次旋转 $\text{[math]}$ ，则第2023次旋转结束时，点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·河南模拟) 如图1，在矩形ABCD中，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 方向运动到点 $\text{[math]}$ 停止，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 方向运动到点 $\text{[math]}$ 停止，若点P，Q同时出发，点 $\text{[math]}$ 的速度为 $\text{[math]}$ ，点 $\text{[math]}$ 的速度为 $\text{[math]}$ ，设运动时间为 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系图象如图2所示，则AC的长为（）

A . 8 B . 9 C . 10 D . 14

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共15分）

11. (2023·河南模拟) 某种试剂的说明书上标明保存温度是 $\text{[math]}$ ，请你写出一个适合该试剂保存的温度：℃.

答案解析收藏纠错 + 选题
12. (2023·河南模拟) 已知点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题

13. (2023·河南模拟) 某校计划从小颖、小亮、小东、小朋四名学生中选拔一人参加全市知识竞赛，下表是他们最近3次选拔测试的平均成绩及方差：

	小颖	小亮	小东	小明
平均成绩/分	97	96	95	97
方差	0.35	0.42	0.36	0.15

学校决定依据他们的平均成绩及稳定性进行选拔，那么被选中的学生应是.

答案解析收藏纠错 + 选题

14. (2023·河南模拟) 如图，在扇形 $\text{[math]}$ 中， $\text{[math]}$ 分别是OA，OB的中点，连接AD和BC交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2023·河南模拟) 如图，正方形ABCD的边长为5，E是边AD上的一动点，将正方形沿CE翻折，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，过点 $\text{[math]}$ 作折痕CE的平行线，分别交正方形ABCD的边于点M，N（点M在点 $\text{[math]}$ 上方），若 $\text{[math]}$ ，则DE的长为.

答案解析收藏纠错 + 选题

三、解答题（本大题共8个小题，共75分）

16. (2023·河南模拟)
1. （1）计算： $\text{[math]}$
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2023·河南模拟) 互联网已成为当代未成年人重要的学习、社交、娱乐工具，对其成长产生深刻影响.2022年11月30日，共青团中央维护青少年权益部、中国互联网络信息中心（CNNIC）、中国青少年新媒体协会联合发布了《2021年全国米成年人互联网使用情况研究报告》（注：此报告中未成年网民指6岁到18岁的在校学生中的网民）.根据报告中的数据，得到以下两幅统计图：

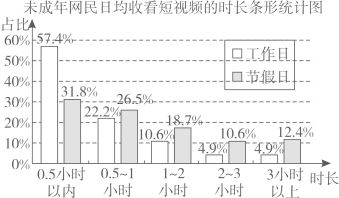
根据以上信息解答下列问题：
1. （1）未成年网民假日收看短视频时长的中位数在范围内，未成年网民收看短视频的内容题材最多的是类。
2. （2）若从全国6岁到18岁的在校生中随机抽取1000人，请分别估计其中工作日和节假日收看短视频的时长在1小时及以上的学生人数。
3. （3）某班为举办“健康上网”的主题班会，从以上统计图中获取了一些信息，请你写出一条获得的信息，并就此提出一条合理的建议。
答案解析收藏纠错 + 选题

18. (2023·河南模拟) 文昌阁位于河南省辉县市区，创建于明代，为八角形三层攒尖顶阁楼，砖木结构.文昌阁是河南省第五批文物保护单位，其建筑结构严谨，造型精巧，工艺精致，气势宏伟，体量高大，是明代木构阁楼建筑的精华，具有重要的历史、科学、艺术价值.某数学兴趣小组准备测量文昌阁阁身的高度，为此制订了测量方案，并利用周末完成了测量，测量结果如下表：

活动课题	测量文昌阁阁身的高度
活动目的	运用三角函数知识解决实际问题
活动工具	测角仪、皮尺等测量工具
示意图
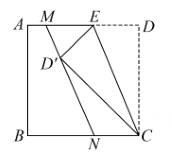
测量步骤	如上图：①利用测角仪在台阶D处测得文昌阁顶点A的仰角为45°； ②利用测角仪在台阶C处测得的文昌阁顶点A的仰角为57°； ③利用皮尺测量每个台阶的高度计算出两处台阶的高度均为1.8m（即点B和点C，点C和点D的垂直距离均为1.8m），利用皮尺测量每个台阶的宽度及点C和点D到台阶边缘的距离计算出点C和点D的水平距离为6.6m（已知A、B、C、D、E均在同一平面内）

请运用所学知识，根据上表中的数据，计算文昌阁阁身AB的高度。（结果取整数.参考数据：sin57°≈0.84，cos57°≈0.54，tan57°≈1.54）

答案解析收藏纠错 + 选题

19. (2023·河南模拟) 某科技小组的同学制作了一个简易台秤（如图1）用来测物体的质量，内部电路如图2所示，其中电流表的表盘被改装为台秤的示数.已知电源电压U为18V，定值电阻R₀为30Ω，电阻R为力敏电阻，其阻值R（Ω）与所受压力F（N）符合反比例函数关系.

（1）请补全下面的表格，在图3中补全点，画出R（Ω）与F（N）的关系图象，并写出阻R（Ω）与压力F（N）的函数关系式.

F（N）	120	▲	60	50	▲	30
R（Ω）	5	6	I0	12	15	20

（2）已知电路中电流 $\text{[math]}$ 与电阻、电源电压的关系式 $\text{[math]}$ ，当电流表的示数达到最大值时，台秤达到量程的最大值.若电流表的量程为 $\text{[math]}$ ，则该台秤最大可称多重的物体？
（3）已知力敏电阻受压力 $\text{[math]}$ 与所测物体的质量 $\text{[math]}$ 的关系为 $\text{[math]}$ .若力敏电阻阻值的变化范围为 $\text{[math]}$ ，则所测物体的质量 $\text{[math]}$ 的变化范围是.

答案解析收藏纠错 + 选题

20. (2023·河南模拟) 国家"双減"政策实施后，某校开展了丰富多彩的社团活动，其中部分同学报名参加了中国象棋和围棋两个社团，该校为参加社团的同学去商场购买中国象棋和围棋.已知购买5副中国象棋和3副围棋共花费165元，购买4副中国象棋和6副围棋共花费240元.
1. （1）求每副中国象棋和围棋的价格各是多少元。
2. （2）在购买时，恰逢商场推出了优惠活动，活动的方案如下：
  方案一：购买围棋不超过20副时，围棋和中国象棋均按原价付款；超过20副时，超过的部分每购买1副围棋赠送1副中国象棋；
  
  方案二：按购买总金额的八折付款.
  
  若该校共需购买40副围棋和 $\text{[math]}$ 副中国象棋，请通过计算说明该校选择哪种方案更划算.
答案解析收藏纠错 + 选题
21. (2023·河南模拟) 如图，在平面直角坐标系xOy中，拋物线 $\text{[math]}$ 的顶点为 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，点 $\text{[math]}$ 是拋物线上一点.
1. （1）求抛物线的表达式及顶点 $\text{[math]}$ 的坐标.
2. （2）当 $\text{[math]}$ 时，求二次函数 $\text{[math]}$ 的最大值与最小值的差.
3. （3）若点 $\text{[math]}$ 是 $\text{[math]}$ 轴上方抛物线上的点（不与点A，B，D重合），设点P的横坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，交直线AD于点 $\text{[math]}$ ，当线段PQ的长随 $\text{[math]}$ 的增大而增大时，请直接写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
22. (2023·河南模拟) 中国是世界上机械发展最早的国家之一.如图1是一辆明代的运输板车，该车沿用宋元制式和包繁式结构，车身选材厚重、纹理精美，低重心的物理结构兼顾了承重性和安全性.如图2是板车侧面的部分示意图，AB为车轮 $\text{[math]}$ 的直径，过圆心O的车架AC一端点 $\text{[math]}$ 着地时，地面CD与车轮 $\text{[math]}$ 相切于点 $\text{[math]}$ ，连接AD，BD.
1. （1）求证：∠ADC=∠DBC.
2. （2）若测得 $\text{[math]}$ ，求AD的长。
答案解析收藏纠错 + 选题
23. (2023·河南模拟) 综合与实践
【问题情境】数学活动课上，老师给出了这样一个问题：

如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，射线AD平分 $\text{[math]}$ ，将射线AD绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到射线 $\text{[math]}$ ，在射线 $\text{[math]}$ 上取点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接BE分别交AD，AC于点M，N，连接CE.问： $\text{[math]}$ 之间的数量关系是什么？线段DM，CN之间的数量关系是什么？

【特例探究】“勤奋”小组的同学们先将问题特殊化，探究过程如下：

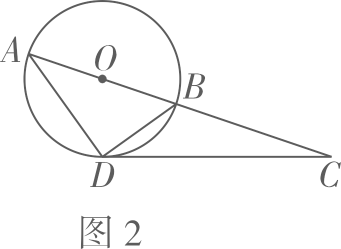
甲同学：当 $\text{[math]}$ 时，如图2，通过探究可以发现， $\text{[math]}$ 都是等腰三角形；

乙同学：可以证明 $\text{[math]}$ ，得到 $\text{[math]}$ ；

丙同学：过点 $\text{[math]}$ 做 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，如图3，则 $\text{[math]}$ ；

丁同学：可以证明 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ， …
1. （1）根据以上探究过程，得出结论：
  ① $\text{[math]}$ 之间的数量关系是；
  
  ②线段DM，CN之间的数量关系是.
2. （2）【类比探究】
  “智慧”小组的同学们在“勤奋”小组的基础上，进一步探究一般情形，当 $\text{[math]}$ 时，如图1，⑴中的两个结论是否仍然成立？如果成立，请仅就图1的情形进行证明；如果不成立，请说明理由。
3. （3）【迁移应用】
  “创新”小组的同学们改变了条件，当 $\text{[math]}$ 时，如图4，若射线AD是 $\text{[math]}$ 的三等分角线， $\text{[math]}$ ，其他条件不变，请直接写出MN的长.
答案解析收藏纠错 + 选题