广东省广州市黄埔区2023年高三模拟考试数学试卷

更新时间：2024-07-14 浏览次数：78 类型：高考模拟

一、单选题

1. (2023·黄埔) 设复数 $\text{[math]}$ 满足 $\text{[math]}$ （ $\text{[math]}$ 是虚数单位），则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·黄埔) 设集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·黄埔) 用一个平行于圆锥底面的平面去截圆锥，截得的圆台上底面半径为1，下底面半径为2，且该圆台侧面积为 $\text{[math]}$ ，则原圆锥的母线长为（）

A . 2 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·黄埔) 函数 $\text{[math]}$ 的大致图象是（）．

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023·黄埔) 南宋数学家杨辉在《详解九章算法》中，研究了二阶等差数列．若 $\text{[math]}$ 是公差不为零的等差数列，则称数列 $\text{[math]}$ 为二阶等差数列．现有一个“三角垛”，共有40层，各层小球个数构成一个二阶等差数列，第一层放1个小球，第二层放3个小球，第三层放6个小球，第四层放10个小球， $\text{[math]}$ ，则第40层放小球的个数为（）

A . 1640 B . 1560 C . 820 D . 780

答案解析收藏纠错 + 选题
6. (2023·黄埔) 若双曲线 $\text{[math]}$ 的两条渐近线与椭圆 $\text{[math]}$ ： $\text{[math]}$ 的四个交点及椭圆 $\text{[math]}$ 的两个焦点恰为一个正六边形的顶点，则椭圆 $\text{[math]}$ 的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·黄埔) 已知可导函数 $\text{[math]}$ 的导函数为 $\text{[math]}$ ，若对任意的 $\text{[math]}$ ，都有 $\text{[math]}$ ，且 $\text{[math]}$ 为奇函数，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
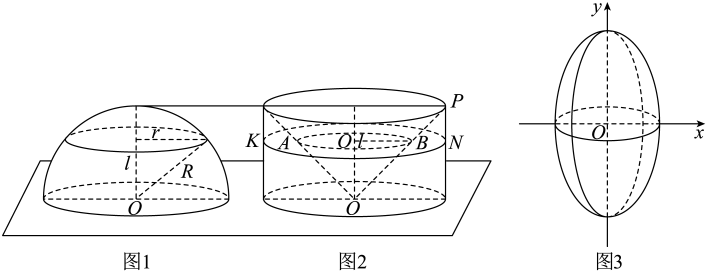
8. (2023·黄埔) 我国南北朝时期的伟大科学家祖暅于5世纪末提出了下面的体积计算原理：“幂势既同，则积不容异”．这就是“祖暅原理”．祖暅原理用现代语言可描述为：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等．运用祖暅原理计算球的体积时，构造一个底面半径和高都与球的半径相等的圆柱，与半球（如图1）放置在同一平面上，然后在圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥后得到一新几何体（如图2），用任何一个平行于底面的平面去截它们时，可证得所截得的两个截面的面积都相等，由此得到新几何体与半球的体积相等，即 $\text{[math]}$ ．现将椭圆 $\text{[math]}$ 绕 $\text{[math]}$ 轴旋转一周后得到如图3所示的椭球，类比上述方法，运用祖暅原理可求得该椭球的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

9. (2023·黄埔) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 在 $\text{[math]}$ 上的投影向量是 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·黄埔) 下列说法正确的是（）

A . 若 $\text{[math]}$ ，则随机变量 $\text{[math]}$ 的方差 $\text{[math]}$ B . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ C . 若随机事件 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 数据5，7，8，11，13，15，17的第80百分位数为15

答案解析收藏纠错 + 选题
11. (2023·黄埔) 已知函数 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ B . 函数 $\text{[math]}$ 的最小正周期为 $\text{[math]}$ C . 函数 $\text{[math]}$ 的图象的对称轴方程为 $\text{[math]}$ D . 函数 $\text{[math]}$ 的图象可由 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ 个单位长度得到

答案解析收藏纠错 + 选题
12. (2023·黄埔) 已知函数 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 在 $\text{[math]}$ 上单调递减 D . $\text{[math]}$ 最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

13. (2023·黄埔) $\text{[math]}$ 的展开式中 $\text{[math]}$ 的系数是（用数字作答）．

答案解析收藏纠错 + 选题
14. (2023·黄埔) 写出经过点 $\text{[math]}$ 且被圆 $\text{[math]}$ 截得的弦长为 $\text{[math]}$ 的一条直线的方程．

答案解析收藏纠错 + 选题
15. (2023·黄埔) 算盘是中国传统的“珠算”工具．下图是一把算盘，自右向左，分别是个位、十位、百位、 $\text{[math]}$ ，上面一粒珠（简称上珠）代表数字 $\text{[math]}$ ，下面一粒珠（简称下珠）代表数字 $\text{[math]}$ ，即五粒下珠的大小等于同组一粒上珠的大小.现从个位和十位这两组中随机选择往下拨一粒上珠，往上拨 $\text{[math]}$ 粒下珠，则算盘表示的数为质数（除了 $\text{[math]}$ 和本身没有其它的约数）的概率是.

答案解析收藏纠错 + 选题

四、双空题

16. (2023·黄埔) $\text{[math]}$ 的内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 的最大值是．

答案解析收藏纠错 + 选题

五、解答题

17. (2023·黄埔) 在△ $\text{[math]}$ 中，角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 及△ $\text{[math]}$ 的面积；
2. （2）再从条件①、条件②这两个条件中选择一个作为已知，求函数 $\text{[math]}$ 的最大值与最小值．
  条件①： $\text{[math]}$ ；条件②： $\text{[math]}$ ．
  
  注：如果选择条件①和条件②分别解答，按第一个解答计分．
答案解析收藏纠错 + 选题

18. (2023·黄埔) 某校为了丰富学生课余生活，组建了足球社团．足球社团为了解学生喜欢足球是否与性别有关，随机抽取了男､女同学各100名进行调查，得到如下列联表：

	喜欢足球	不喜欢足球	合计
男生	60	40	100
女生	30	70	100
合计	90	110	200

（1）根据小概率值 $\text{[math]}$ 的 $\text{[math]}$ 独立性检验，判断是否有 $\text{[math]}$ 的把握认为该校学生喜欢足球与性别有关？

（2）现从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门．已知男生进球的概率为 $\text{[math]}$ ，女生进球的概率为 $\text{[math]}$ ，每人射门一次，假设各人射门相互独立，求3人进球总次数 $\text{[math]}$ 的分布列和均值．

附： $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

答案解析收藏纠错 + 选题

19. (2023·黄埔) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023·黄埔) 如图，在几何体 $\text{[math]}$ 中，矩形 $\text{[math]}$ 所在平面与平面 $\text{[math]}$ 互相垂直，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的平面角的余弦值．
答案解析收藏纠错 + 选题
21. (2023·黄埔) 直线 $\text{[math]}$ 经过点 $\text{[math]}$ $\text{[math]}$ 且与抛物线 $\text{[math]}$ 交于 $\text{[math]}$ 两点．
1. （1）若 $\text{[math]}$ ，求抛物线 $\text{[math]}$ 的方程；
2. （2）若直线 $\text{[math]}$ 与坐标轴不垂直， $\text{[math]}$ ，证明： $\text{[math]}$ 的充要条件是 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023·黄埔) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求函数 $\text{[math]}$ 的单调区间；
2. （2）讨论函数 $\text{[math]}$ 的零点个数．
答案解析收藏纠错 + 选题