一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
-
A .  B . 2
C .
B . 2
C .  D . 4
D . 4
-
A .  ,
,  都平行于同一个平面
B .
都平行于同一个平面
B .  ,
,  与同一个平面所成角相等
C .
与同一个平面所成角相等
C .  ,
,  都垂直于同一个平面
D .
都垂直于同一个平面
D .  平行于
平行于 所在平面
所在平面
-
A . 矩形
B . 菱形
C . 正方形
D . 平行四边形
-
5.
(2024高一下·江阴月考)
某同学投掷一枚骰子5次,分别记录每次骰子出现的点数,已知这组数据的平均数为3,方差为0.4,则点数2出现的次数为( )
A . 0
B . 1
C . 2
D . 3
-
-
7.
(2023高一下·温州期末)
在一个盒子中有红球和黄球共5个球,从中不放回的依次摸出两个球,事件

“第二次摸出的球是红球”,事件
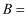
“两次摸出的球颜色相同”,事件

“第二次摸出的球是黄球”,若

, 则下列结论中错误的是( )
-
8.
(2023高一下·温州期末)
如图,在长方体

中,

,

,

为棱

上一点,且

, 平面

上一动点

满足

, 设

是该长方体外接球上一点,则

,

两点间距离的最大值是( )

二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
-
10.
(2023高一下·温州期末)
国家统计网最新公布的一年城市平均气温显示昆明与郑州年平均气温均为16.9摄氏度,该年月平均气温如下表所示,并绘制如图所示的折线图,则( )
|
月份
|
1月
|
2月
|
3月
|
4月
|
5月
|
6月
|
7月
|
8月
|
9月
|
10月
|
11月
|
12月
|
|
昆明
|
9.3
|
12.4
|
16.5
|
19
|
21.6
|
21.5
|
21.3
|
21.2
|
20.4
|
16.8
|
12.4
|
10.5
|
|
郑州
|
2.9
|
8.7
|
11.9
|
16.5
|
23.6
|
28.9
|
28.6
|
26.7
|
23.1
|
15.2
|
11.3
|
5.7
|

A . 昆明月平均气温的极差小于郑州月平均气温的极差
B . 昆明月平均气温的标准差大于郑州月平均气温的标准差
C . 郑州月平均气温的中位数小于昆明月平均气温的中位数
D . 郑州月平均气温的第一四分位数为10
-
A .  的最小值为
的最小值为 B .
B .  的最小值为
的最小值为 C .
C .  的最大值为
的最大值为 D .
D .  的最大值为
的最大值为
-
三、填空题(本大题共4小题,共20.0分)
-
13.
(2023高一下·温州期末)
如图,由

,

两个元件组成并联电路,观察两个元件正常或失效的情况,则事件

“电路是通路”包含的样本点个数为
.

-
-
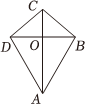
15.
(2023高一下·温州期末)
“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美,如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”,则直线

与平面

所成角的正弦值为
.

-
16.
(2023高一下·温州期末)
如图,四边形

为筝形

有一条对角线所在直线为对称轴的四边形

, 满足

,

的中点为

,

, 则筝形

的面积取到最大值时,

边长为
.
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
-
(1)
求

的值;
-
(2)
设

,

在复平面内所对应的点分别为

,

, 求线段

的长度.
-
-
-
(2)
若

, 求

的值.
-
-
(1)
求圆柱

的表面积;
-
-
20.
(2024高一下·杭州月考)
现行国家标准

中规定了10大类食品中重金属汞的污染限量值,其中肉食性鱼类及其制品中汞的最大残留量为

, 近日某水产市场进口了一批冰鲜鱼2000条,从中随机抽取了200条鱼作为样本,检测鱼体汞含量与其体重的比值

, 由测量结果制成如图所示的频率分布直方图.

-
(1)
求

的值,并估计这200条鱼汞含量的样本平均数;
-
(2)
用样本估计总体的思想,估计进口的这批鱼中共有多少条鱼汞含量超标;
-
(3)
从这批鱼中顾客甲购买了2条,顾客乙购买了1条,甲乙互不影响,求恰有一人购买的鱼汞含量有超标的概率.
-
-
(1)
若

, 求

的大小;
-
(2)
若

, 过

作

的垂线交

于

, 求

的取值范围.
-
-
(1)
当

时,求证:

;
-
(2)
当线段

的长度最小时,求二面角

的正弦值.
 B .
B . 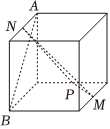 C .
C . 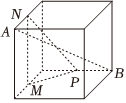 D .
D . 


