一、选择题(共12小题,每小题3分,共36分,在每小题都给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目答案标号涂黑.)
-
-
-
A . 20°
B . 70°
C . 90°
D . 110°
-
A . x轴正半轴
B . x轴负半轴
C . y轴正半轴
D . y轴负半轴
-
A . 检测长征运载火箭的零部件质量情况
B . 了解全国中小学生课外阅读情况
C . 调查某批次汽车的抗撞击能力
D . 检测某城市的空气质量
-
-
-
-
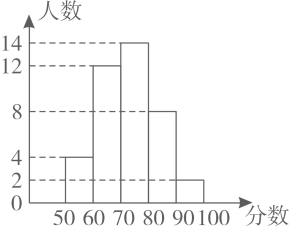
A . 得分在90~100分之间的人数最少
B . 该班的总人数为40
C . 及格(≥60分)人数是26
D . 得分在70~80分之间的人数最多
-
10.
(2024九下·武威模拟)
《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?设有

辆车,人数为

,根据题意可列方程组为( )
-
-
A . 270°
B . 360°
C . 540°
D . 560°
二、填空题(本答题共6小题,每小题2分,共12分.)
-
-
-
-
-
17.
(2023七下·邕宁期末)
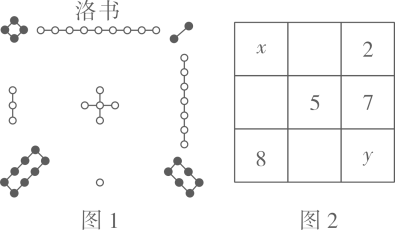
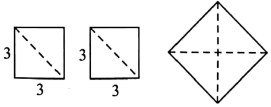
把1~9这九个数填入3×3的方格中,使其任意一行,任意一列及任意对角线上的数之和都相等,这样便构成一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”,(图2)是仅可以看到部分数值的“九宫格”,则x-y的值为
.
-
18.
(2023七下·邕宁期末)
在平面直角坐标系

中,对于点

如果点

的纵坐标满足

那么称点

为点

的“关联点”.例如点

的“关联点”的坐标为

;如果点

的关联点

坐标为

则点

的坐标为
.
三、解答题(本大题共8小题,共72分,解答应写出文字说明、证明过程或演算步骤.)
-
-
-
-
22.
(2023七下·邕宁期末)
按要求完成下列证明:
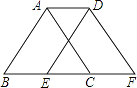
已知:如图, , 直线AE交直线CD于点C,∠BAC+∠CDF=180°.
, 直线AE交直线CD于点C,∠BAC+∠CDF=180°.
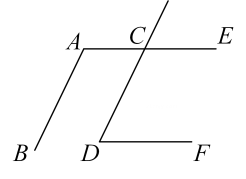
求证: .
.
证明:∵ (① )
(① )
∴∠BAC=∠DCE(② )
∵∠BAC+∠CDF=180°(已知),
∴③ ▲ +∠CDF=180°(④ )
∴ (⑤ )
(⑤ )
-
23.
(2023七下·邕宁期末)
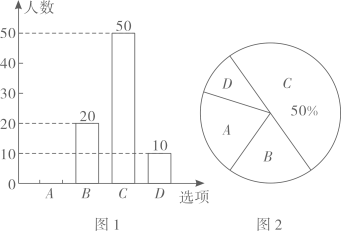
随着科技的不断发展,越来越多的中学生拥有了自己的手机.中学生应合理使用手机,沉迷于手机,将会影响我们的生活和学习.某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查衷如图所示),并用调查结果绘制了图1、图2两种“周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
中学生每周使用手机的时间问卷调查表
|
选项
|
使用时间/(小时)
|
|
|
A
|
0<t≤2
|
|
|
B
|
2<t≤2.5
|
|
|
C
|
2.5<t≤3
|
|
|
D
|
t>3
|
|
您好!这是一份关于您平均每周使用手机人数时间的问调查表,请在表中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作。
|
-
(1)
本次接受问卷调查的共有人;在扇形统计图中“D”选项所占的百分比;
-
(2)
扇形统计图中,“B”选项所对应扇形圆心角为度;
-
-
(4)
若该校共有1200名中学生,请你估计该校使用手机的时间在“A”选项的有多少名学生?
-
24.
(2023七下·邕宁期末)
列方程或不等式组解应用题:
某旅游商品经销店欲购进A、B两种纪念品,若用380元可以购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件.
-
-
(2)
若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出后总获利不低于216元,问应该怎样进货,才能使总获利最大?
-
-
(1)
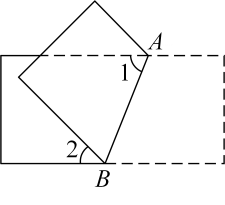
若BC平分∠ABD,∠D=100°,求∠ABC的度数;
-
(2)
若∠1=∠2,求证:

.
-
-
(1)
在平面直角坐标系xOy中,若点A的坐标为(2,4),点B的坐标为(6,4),连接AB,请直接写出线段AB的长度及直线AB与x轴的位置关系;
-
(2)
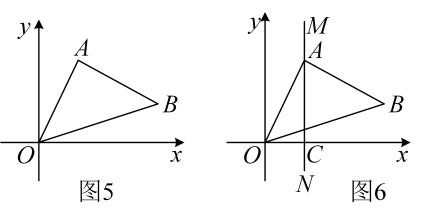
如图5,△AOB中,若A,B两点的坐标分别为(2,4),(6,2),求△AOB的面积;
-
(3)
如图6,在(2)的条件下,若直线MN经过点C(2,0)且垂直x轴,那么在直线MN上是否存在点P(除A点外),使得△OBP的面积等于△AOB的面积,若存在,请求出P点坐标、若不存在,请说明理由。
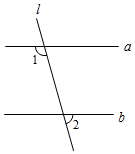

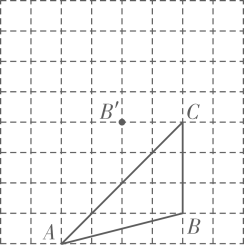
经过平移后得到
, 图中标出了点
的对应点
, 补全
;
的高
;
则四边形
的面积为 ▲ ;
的坐标为
则点
的坐标为 ▲ .
, 直线AE交直线CD于点C,∠BAC+∠CDF=180°.

.
(① )
(⑤ )

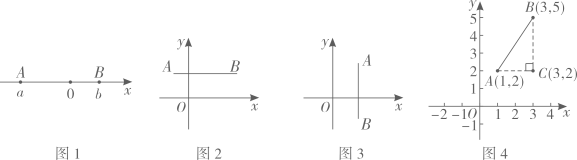
在点
的右侧,则
, 类似的,在平面直角坐标系xOy中,点
的坐标为
, 点
的坐标为
,
轴,则
.
轴,则
.
, 则
.