重庆110中教育集团三校联考2023-2024学年八年级上学...

更新时间：2024-01-24 浏览次数：35 类型：期中考试

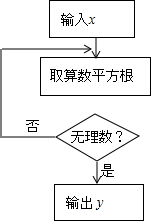
一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1. (2023八上·重庆市期中) 下列实数中，是无理数的是（　　）

A . 1.010010001 B . $\text{[math]}$ C . $\text{[math]}$ D . 3.14

答案解析收藏纠错 + 选题
2. (2024八下·辽阳期中) 以下列长度的线段不能围成直角三角形的是（）

A . 5，12， 13 B . $\text{[math]}$ C . $\text{[math]}$ ，3，4 D . 2，3，4

答案解析收藏纠错 + 选题
3. (2023八上·重庆市期中) 下列运算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·重庆市期中) 下列四个图象中， $\text{[math]}$ 不是 $\text{[math]}$ 的函数的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023八上·重庆市期中) 如图，用边长为3的两个小正方形拼成一个大正方形，则大正方形的边长最接近的整数是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
6. (2023八上·重庆市期中) 在△ABC中，∠C=90°，沿AD折叠△ABC，点C恰好落在AB边上的E点，已知DE=4，BE=3，则AC的长度是（　　）

A . 14 B . 12 C . 10 D . 8

答案解析收藏纠错 + 选题
7. (2023八上·重庆市期中) 如图，正方体的棱长为6cm，A是正方体的一个顶点，B是侧面正方形对角线的交点，一只蚂蚁在正方体的表面上爬行，从点A爬到点B的最短路径长是（）

A . 12cm B . ( $\text{[math]}$ +6)cm C . $\text{[math]}$ cm D . 9cm

答案解析收藏纠错 + 选题
8. (2023八上·重庆市期中) 如图，在Rt△ABC中，∠ACB=90°，AC= $\text{[math]}$ ，将其绕B点顺时针旋转一周，则分别以BA、BC为半径的圆形成一个圆环，则该圆环的面积为（　　）

A . $\text{[math]}$ B . 2π C . 4π D . 6π

答案解析收藏纠错 + 选题
9. (2023八上·重庆市期中) 如图，在长方形ABCD中，AB=6，AD=4，DM=2，动点P从点A出发，沿路径A→B→C→M运动，则△AMP的面积y与点P经过的路径长x之间的函数关系用图象表示大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2023八上·重庆市期中) 若 $\text{[math]}$ （n为正整数），则下列说法正确的个数是（　　）
① $\text{[math]}$ ；
② $\text{[math]}$ ；
③ $\text{[math]}$ ．

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题

二、填空题：（本题共8小题，共32分）请将每小题答案填写在答题卡中对应横线上.

11. (2023八上·重庆市期中) 实数27的立方根是．

答案解析收藏纠错 + 选题
12. (2023八上·重庆市期中) 有一个数值转换器，原理如图所示，当输入的数为16时，输出的数为．

答案解析收藏纠错 + 选题
13. (2024八上·广陵期末) 已知一次函数y＝2x﹣1的图象经过A（x₁ ， 1），B（x₂ ， 3）两点，则x₁x₂（填“＞”“＜”或“＝”）.

答案解析收藏纠错 + 选题
14. (2023八上·重庆市期中) 一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度，其中x表示时间，y表示水位高度.

x/h

0

1

2

3

4

5

y/m

3

3.3

3.6

3.9

4.2

4.5

根据表格中水位的变化规律，则y与x的函数表达式为.

答案解析收藏纠错 + 选题
15. (2023八上·重庆市期中) 已知点 P 在第四象限，该点到 x 轴的距离为 3，到 y 轴的距离为 1，则点 P的坐标为.

答案解析收藏纠错 + 选题
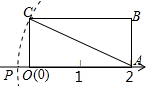
16. (2023八上·重庆市期中) 如图，长方形OABC放在数轴上，OA=2，OC=1，以A为圆心，AC长为半径画弧交数轴于P点，则P点表示的数为

答案解析收藏纠错 + 选题
17. (2023八上·重庆市期中) 某地植物园从正门到侧门有一条小路，甲徒步从正门出发匀速走向侧门，出发一段时间开始休息，休息了0.6小时后仍按原速继续行走，乙与甲同时出发，骑自行车从侧门匀速前往正门，到达正门后休息0.2小时，然后按原路原速匀速返回侧门．图中折线分别表示甲、乙到侧门的距离y（km）与出发时间x（h）之间的关系图象．结合图象，当乙回到侧门时，甲与侧门的距离是千米．

答案解析收藏纠错 + 选题
18. (2023八上·重庆市期中) 如图，直线y=2x+4与x轴、y轴分别交于A、B两点，点C是第二象限内一点，△ABC为等腰直角三角形且∠C=90°，则直线BC的解析式为．

答案解析收藏纠错 + 选题

三、解答题：（本大题8个小题，除19题8分外，其余各小题各10分，共78分）请将解答过程书写在答题卡中对应的位置上。

19. (2023八上·重庆市期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023八上·重庆市期中) 已知：如图，线段AD、BF相交于点H，∠A=∠D，点E是线段AB上一点．
1. （1）用直尺和圆规，以点E为顶点，EA为一边，在线段AB下方作∠AEC，使∠AEC=∠B，边EC与DF的延长线相交于点C．（要求：尺规作图，不写作法和结论，保留作图痕迹）
2. （2）在（1）的情况下，求证：∠C＝∠B（请完成以下证明过程）．
  证明：∵∠AEC＝∠B ，
  ∴    ▲    ∥    ▲     ，
  ∴∠C＝∠BFD ，
  ∵∠A＝∠D ，
  ∴    ▲    ∥    ▲     ，
  ∴    ▲    ＝    ▲     ，
  ∴∠C＝∠B ．
答案解析收藏纠错 + 选题
21. (2023八上·重庆市期中) 如图，在直角坐标系中，△ABC的位置如图所示，请回答下列问题：
1. （1）请直接写出A、B、C三点的坐标、、．
2. （2）画出△ABC关于x轴的对称图形△A₁B₁C₁ ．
3. （3） △ABC的面积为．
4. （4）已知P为x轴上一动点，则AP+BP的最小值为．
答案解析收藏纠错 + 选题
22. (2023八上·重庆市期中) 如图，在离水面高度为6米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长度为AC的3倍．
1. （1）求此时船离岸边AB的长；（结果保留根号）
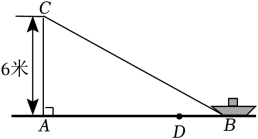
2. （2）若此人以0.5米/秒的速度收绳，12秒后船移动到点D的位置．则船向岸边移动了大约多少米？（假设绳子是直的，结果精确到0.1米，参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73）
答案解析收藏纠错 + 选题
23. (2023八上·重庆市期中) 我们规定用（a ， b）表示有序数对．给出如下定义：记 $\text{[math]}$ ， $\text{[math]}$ ，其中a＞0， b＞0，将（m ， n）与（n ， m）称为有序数对（a ， b）的一对“对称数对”．例如：（4，1）的一对“对称数对”为 $\text{[math]}$ 和 $\text{[math]}$ ．
1. （1）有序数对（4，3）的一对“对称数对”是；
2. （2）若有序数对（5，y）的一对“对称数对”相同，则y的值为；
3. （3）若有序数对（x ， 2）的一个“对称数对”是 $\text{[math]}$ ，则x的值为；
4. （4）若有序数对（a ， b）的一个“对称数对”是 $\text{[math]}$ ，求ab的值．
答案解析收藏纠错 + 选题
24. (2023八上·重庆市期中) 某音乐平台的收费标准主要包括会员和非会员两种收费方式．会员付费一个月9元会费，下载歌曲，每首另付费2元：非会员下载歌曲无会费，每首付费5元．王先生打算在这个音乐平台下载歌曲．
设他下载的歌曲每月为x（首），选择会员每月费用为y₁（元），非会员每月费用为y₂（元）．
1. （1）请直接写出y₁ ， y₂与x之间的关系式；
2. （2）在给出的平面直角坐标系中，画出y₁ ， y₂的图象；
3. （3）根据画出的函数图象填空：当下载的歌曲时，选择会员与非会员费用相当；当下载的歌曲时，选择会员合算；当下载的歌曲时，选择非会员合算．
答案解析收藏纠错 + 选题
25. (2023八上·重庆市期中) 如图1，四边形ADCO中，∠AOC=90°，∠ADC=90°，AD=7，DC=24，CO=15．
1. （1）求线段AO的长度；
2. （2）如图2所示，OB是∠AOC的平分线，一动点P从点O出发，以每秒2个单位长度的速度沿射线OB运动．设点P的运动时间为t秒，当△AOP是等腰三角形时，请求出t的值．
答案解析收藏纠错 + 选题
26. (2023八上·重庆市期中) 已知直线 $\text{[math]}$ 与x轴交于点A（-6，0），与y轴交于点B ．
1. （1）求b的值；
2. （2）把△AOB绕原点O顺时针旋转90°后，点A落在y轴的A′处，点B落在x轴的B'处；
  ①求直线A'B'的函数关系式；
  ②设直线AB与直线A'B'交于点C ，长方形PQMN的顶点都在△AB'C的边上，其中点P ， Q在线段AB'上，点M在线段B'C上，点N在线段AC上．若长方形PQMN的两条邻边的比为1：2，求长方形PQMN的周长．
答案解析收藏纠错 + 选题