四川省成都市简阳市2022-2023学年七年级下学期期中数学...

更新时间：2023-10-16 浏览次数：45 类型：期中考试

一、选择题（本大题共8个小题，每小题4分，共32分）

1. (2023七下·四川期中) 下列计算正确的是（）

A . x³÷x²＝x B . x³•x²＝x⁶ C . x³+x²＝x⁵ D . （x³）²＝x⁹

答案解析收藏纠错 + 选题
2. (2023七下·四川期中) 在下列数学符号中，表示“两条直线互相垂直”的符号是（）

A . ∠ B . $\text{[math]}$ C . ⊥ D . ≌

答案解析收藏纠错 + 选题
3. (2023七下·四川期中) 随着北斗系统全球组网的步伐，北斗芯片的研发生产技术也在逐步成熟，国产北斗芯片可支持接收多系统的导航信号，应用于自动驾驶、无人机、机器人等高精度定位需求领域，将为中国北斗导航产业发展提供有力支持，目前，该芯片工艺已达22纳米（即0.000000022米），则数据0.000000022用科学记数法表示为（）

A . 0.22×10^-7 B . 2.2×10^-8 C . 2.2×10^-9 D . 22×10^-8

答案解析收藏纠错 + 选题
4. (2023七下·四川期中) 已知∠A的余角为50°，则∠A的度数为（）

A . 180° B . 90° C . 50° D . 40°

答案解析收藏纠错 + 选题
5. (2023七下·四川期中) 如图，将一直角三角尺与两边平行的纸条按如图所示放置，其中说法不正确的是（）

A . ∠1＝∠2 B . ∠3＝∠4 C . ∠1＝∠4 D . ∠4+∠5＝180°

答案解析收藏纠错 + 选题
6. (2023七下·四川期中) 已知a≠0，则 $\text{[math]}$ 的值（）

A . 等于0 B . 等于1 C . 小于1 D . 大于1

答案解析收藏纠错 + 选题
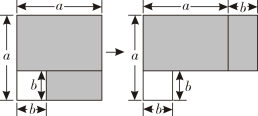
7. (2023七下·四川期中) 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，再将剩下的阴影部分剪开，拼成右边的长方形.根据图形的变化过程可以验证下列哪一个等式成立?（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·四川期中) 向一个容器内以固定的速度注入水，液面升高的高度h与注水时间t的图像大致如图所示，则符合图象条件的容器为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题4分，共20分）

9. (2023七下·四川期中) 如图，两条直线a ， b相交. 已知∠1=50°，则∠2=，∠3=.

答案解析收藏纠错 + 选题
10. (2023七下·四川期中) 若a^m=2，aⁿ=5，则a^m+n等于．

答案解析收藏纠错 + 选题
11. (2023七下·四川期中) 三角板是我们学习数学的好帮手，将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，则∠CBD的度数为．

答案解析收藏纠错 + 选题
12. (2023七下·四川期中) 一个底面是正方形的长方体，高为4cm，底面正方形边长为3cm．如果它的高不变，把底面正方形边长增加了xcm，则所得长方体增加的体积V（cm³）与x（cm）之间的关系式是．

答案解析收藏纠错 + 选题
13. (2023七下·四川期中) 如图，已知AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，交AB于H，∠AGE=50°，则∠BHF=．

答案解析收藏纠错 + 选题

三、解答题（本大题共5个小题，共48分）

14. (2023七下·四川期中)
1. （1）计算：（﹣2）³﹣（2022﹣π）⁰+（ $\text{[math]}$ ）^﹣²﹣|﹣5|；
2. （2）先化简，再求值：[（x+y）²﹣（3x﹣y）（3x+y）﹣2y²]÷（﹣2x），其中x＝﹣1，y＝﹣2．
答案解析收藏纠错 + 选题
15. (2023七下·四川期中) 推理填空．
已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．
证明： $\text{[math]}$
$\text{[math]}$
$\text{[math]}$ DG∥AC（）
$\text{[math]}$ _▲_ ．（）
$\text{[math]}$ ．（）
$\text{[math]}$ _▲_ ．（）
$\text{[math]}$ EF∥CD ．（）
$\text{[math]}$ ．（）
$\text{[math]}$ ，
$\text{[math]}$ ，
$\text{[math]}$ ，
$\text{[math]}$ ． (垂直的定义)

答案解析收藏纠错 + 选题
16. (2023七下·四川期中) 已知：如图，点C在∠MON的一边OM上，过点C的直线AB∥ON，CD平分∠ACM，CE⊥CD.
1. （1）若∠O＝50°，求∠BCD的度数；
2. （2）求证：CE平分∠OCA；
3. （3）当∠O为多少度时，CA分∠OCD成1：2两部分，并说明理由.
答案解析收藏纠错 + 选题
17. (2023七下·四川期中) “五一”小长假期间，小天和父母一起开车到距家220千米的景点旅游，出发前，汽车油箱内储油45升，当行驶了180千米时，发现油箱余油量为27升（假设行驶过程中汽车的耗油量是均匀的）．
1. （1）求该车平均每千米的耗油量；
2. （2）写出油箱余油量Q（升）与行驶路程x（千米）的关系式；
3. （3）当油箱中剩余油量低于3升时，汽车将自动报警，如果往返途中不加油，他们能否在汽车报警前沿原路返回到家？请说明理由．
答案解析收藏纠错 + 选题
18. (2023七下·四川期中) 数学活动课上，张老师准备了若干个如图①的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b ，宽为a的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图②的大正方形．
1. （1）观察图②，请你写出代数式（a+b）² ， a²+b² ， ab之间的等量关系是；
2. （2）根据（1）中的等量关系，解决下列问题；
  ①已知a+b＝4，a²+b²＝10，求ab的值；
  
  ②已知（x-2021）²+（x-2019）²＝52，求x-2020的值．
答案解析收藏纠错 + 选题

四、填空题（本大题共5个小题，每小题4分，共20分）

19. (2023七下·四川期中) 已知2^x÷2^y＝8，则x﹣y+1=．

答案解析收藏纠错 + 选题
20. (2023七下·四川期中) $\text{[math]}$ 和 $\text{[math]}$ 互余， $\text{[math]}$ 和 $\text{[math]}$ 互补， $\text{[math]}$ ， $\text{[math]}$ 度．

答案解析收藏纠错 + 选题
21. (2024七下·邛崃期末) 某学习小组在“设计自己的运算程序”这一综合与实践课题的研究中发现，任意写下一个三位数（三位数字相同的除外），重新排列各位数字，使其组成一个最大的数和一个最小的数，然后用最大的数减去最小的数，得到差．重复这个过程，就能得到一个固定的数字，他们称它为“数字黑洞”．这个固定的数字是．

答案解析收藏纠错 + 选题
22. (2023七下·四川期中) 如图，折叠一张上下边沿互相平行的纸片，测得 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
23. (2023七下·四川期中) 如图1，正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上有一定点 $\text{[math]}$ ，连接 $\text{[math]}$ .动点 $\text{[math]}$ 从正方形的顶点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 以1cm/s的速度匀速运动到终点 $\text{[math]}$ .图2是点 $\text{[math]}$ 运动时， $\text{[math]}$ 的面积y（cm²）随时间x（s）变化的全过程图象，则 $\text{[math]}$ 的长度为cm.

答案解析收藏纠错 + 选题

五、解答题（本大题共3个小题，共30分）

24. (2023七下·四川期中) 有八张完全相同的直角三角形纸片，如图1所示，其边长分别为a，b，c，且a＜b＜c．现将其中四张纸片拼得如图2所示的正方形A₁B₁C₁D₁和正方形A₂B₂C₂D₂ ．
1. （1）正方形A₁B₁C₁D₁的边长为．
2. （2）请你用两种不同的方法表示正方形A₂B₂C₂D₂面积，并写出a² ， b² ， c²之间的数量关系．
3. （3）若将剩余的四张纸片按图3的方式拼在图2外围，可得正方形A₃B₃C₃D₃ ．若正方形A₁B₁C₁D₁的面积为49，正方形A₃B₃C₃D₃的面积为289，求正方形A₂B₂C₂D₂的面积．
答案解析收藏纠错 + 选题
25. (2023七下·四川期中) 如图1，将南北向的天府大道与东西向的海洋路看成两条相互垂直的直线，十字路口记作点A．小明从海洋路上的点B出发，骑车向西匀速直行；与此同时，小颖从点A出发，沿天府大道步行向北匀速直行，小明到达A点处遇到红灯，等待1分钟后，他提速25%继续骑行．设出发x分钟时，小明、小颖两人与点A的距离分别为y₁米和y₂米．已知y₁ ， y₂与x之间的图象如图2所示．
1. （1）小明提速后骑车的速度为米/分，小颖步行的速度为米/分；
2. （2）当6≤x≤10时，分别写出y₁ ， y₂与x的关系式；
3. （3）出发多少分钟后，小明、小颖离A点的距离相等？
答案解析收藏纠错 + 选题
26. (2023七下·四川期中) 已知直线MN∥PQ，点A是直线MN上一个定点，点B在直线PQ上运动．点H为平面上一点，且满足∠AHB＝90°．设∠HBQ＝α．
1. （1）如图1，当α＝70°时，求∠HAN的度数．
2. （2）过点H作直线l平分∠AHB ，直线l交直线MN于点C ．
  ①如图2，当α＝60°时，求∠ACH的度数；
  
  ②当∠ACH＝30°时，求出α的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

四川省成都市简阳市2022-2023学年七年级下学期期中数学...

副标题：

*注意事项：

四川省成都市简阳市2022-2023学年七年级下学期期中数学...

试题分析

总体分析

题量分析

难度分析

知识点分析