广东省深圳市南山区2022-2023学年八年级下学期期末数学...

更新时间：2024-07-14 浏览次数：146 类型：期末考试

一、选择题（本部分共10小题，每小题3分，共30分，每小题给出4个选项，其中只有一个是正确的）

1. (2023九上·光明开学考) 若代数式 $\text{[math]}$ 有意义，则x的取值范围是（　　）

A . x＝0 B . x＝3 C . x≠0 D . x≠3

答案解析收藏纠错 + 选题
2. (2024八下·福田月考) 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）

A . 斐波那契螺旋线 B . 笛卡尔心形线 C . 赵爽弦图 D . 科克曲线

答案解析收藏纠错 + 选题
3. (2023七下·保山期末) 若a＞b，则下列不等式成立的是（　　）

A . a-5＜b-5 B . -2a＜-2b C . $\text{[math]}$ D . a²＞b²

答案解析收藏纠错 + 选题
4. (2023九上·光明开学考) 下列从左到右的变形为因式分解的是（　　）

A . xy²（x-1）＝x²y²-xy² B . （a+3）（a-3）＝a²-9 C . 2023a²-2023＝2023（a+1）（a-1） D . x²+x-5＝（x-2）（x+3）+1

答案解析收藏纠错 + 选题
5. (2023八下·南山期末) 如图，将直角△ABC沿边AC的方向平移到△DEF的位置，连结BE，若CD＝6，AF＝14，则BE的长为（　　）

A . 4 B . 6 C . 8 D . 12

答案解析收藏纠错 + 选题
6. (2023八下·南山期末) 如图，小明从点A出发沿直线前进10米到达点B，向左转45°后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D…照这样走下去，小明第一次回到出发点A时所走的路程为（　　）

A . 100米 B . 80米 C . 60米 D . 40米

答案解析收藏纠错 + 选题
7. (2023八下·南山期末) 如图，已知锐角∠AOB按下列步骤图：
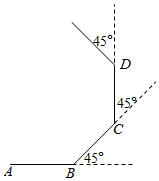
①在射线OA上取一点C，以点O为圆心，OC长为半径作圆弧DE，交射线OB与点F，连接CF；②以点F为圆心，CF长为半径作弧，交弧DE于点G；③连接FG，CG．作射线OG．根据以上作图过程及所作图形，下列结论中错误的是（　　）

A . OG＝OC B . ∠OCF＝∠OGF C . OF垂直平分CG D . CG＝2FG

答案解析收藏纠错 + 选题
8. (2023八下·南山期末) 下列四个命题中，假命题是（）

A . 顺次连接四边形各边中点所得四边形是平行四边形 B . 斜边和一条直角边分别相等的两个直角三角形全等 C . 等腰三角形的高、中线、角平分线互相重合 D . 一组对边平行，一组对角相等的四边形是平行四边形

答案解析收藏纠错 + 选题
9. (2023八下·南山期末) 直线l₁：y＝k₁x+b与直线l₂：y＝k₂x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k₂x＞k₁x+b的解集为（　　）

A . x＞3 B . x＜3 C . x＞-1 D . x＜-1

答案解析收藏纠错 + 选题
10. (2023八下·南山期末) 某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其它费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高（　　）

A . $\text{[math]}$ B . 30% C . 35% D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（共5小题）

11. 分解因式：xy²-4x＝．

答案解析收藏纠错 + 选题
12. (2023八下·南山期末) 关于x的方程3x+a＝x-7的根是正数，则实数a的取值范围是．

答案解析收藏纠错 + 选题
13. (2023九上·光明开学考) 如图，在△ABC中，∠B＝65°，∠BAC＝75°，△ABC绕点A按逆时针方向旋转到△ADE的位置，点D在BC边上，DE交AC于点F，则∠AFD＝．

答案解析收藏纠错 + 选题
14. (2023八下·南山期末) 如图，在平行四边形纸片ABCD中，AB＝3，将纸片沿对角线AC对折，BC边与AD边交于点E，此时，△CDE恰为等边三角形，则图中重叠部分的面积为．

答案解析收藏纠错 + 选题
15. (2023九上·光明开学考) 如图，在Rt△ABC中，∠ABC＝90°，过点B作BE⊥AC，延长BE到点D，使得 BD＝AC，连接AD，CD，若AB＝4，AD＝5，则CD的长为．

答案解析收藏纠错 + 选题

三、解答题（共7小题）

16. (2023八下·南山期末)
1. （1）解不等式：3-x＜2x+6；
2. （2）解分式方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2023八下·南山期末) 解不等式组： $\text{[math]}$ ，并在数轴上表示出它的解集．

答案解析收藏纠错 + 选题
18. (2023八下·南山期末) 先化简，再求值： $\text{[math]}$ ，其中x＝4．

答案解析收藏纠错 + 选题
19. (2023八下·南山期末) 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（-2，4），B（-4，1），C（0，1）．

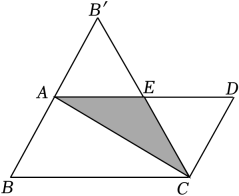
⑴画出与△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

⑵画出以C₁为旋转中心，将△A₁B₁C₁逆时针旋转90°后的△A₂B₂C₂；

⑶尺规作图：连接A₁A₂ ，在C₁A₂边上求作一点P，使得点P到A₁A₂的距离等于PC₁的长（保留作图痕迹，不写作法）；

⑷请直接写出∠C₁A₁P的度数为．

答案解析收藏纠错 + 选题
20. (2023八下·南山期末) 如图，在▱ABCD中，点O是对角线AC的中点．某数学学习小组要在AC上找两点E，F，使四边形BEDF为平行四边形，现总结出甲、乙两种方案如下：

甲方案

乙方案

分别取AO，CO的中点E，F

作BE⊥AC于点E，DF⊥AC于点F

请回答下列问题：
1. （1）以上方案能得到四边形BEDF为平行四边形的是 ▲ ，选择其中一种并证明，若不能，请说明理由；
2. （2）若EF＝2AE，S_△_AED＝6，求▱ABCD的面积．
答案解析收藏纠错 + 选题
21. (2023八下·南山期末) 为了方便乘客出行，深圳宝安国际机场安装了图1所示的平地电梯，如图2是其示意图，已知电梯AB的长度为200米，小刚和小明两人不乘电梯在地面匀速行走时，小刚每分钟行走的路程是小明的1.2倍，且1.5分钟后，小刚比小明多行走15米．
1. （1）求两人在地面上每分钟各行走多少米？
2. （2）若两人同时从A点出发在平地电梯上行走，电梯向前行驶的同时两人仍保持原来在地面上匀速行走的速度在电梯上行走，当小刚到达B处时，小明还剩20米才到达B处．
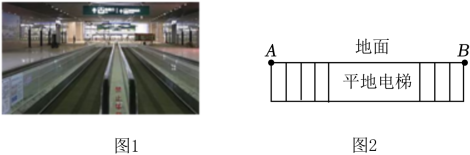
  ①求电梯每分钟行驶多少米？
  ②当小刚到达B处时，发现有一袋行李忘在了A处，于是马上以每分钟a米的速度从地面返回A处，拿了行李后立即乘平地电梯（同时按原来在地面上匀速行走的速度行走）去B处和小明汇合，要使小明到达B点后等待的时间不超过4分钟，求a的最小值．
答案解析收藏纠错 + 选题
22. (2023八下·南山期末) [知识链接]，“化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法，通过“转化、化归”通常可以实现化未知为已知，化复杂为简单，从而使问题得以解决．在探究平行四边形的性质时，学习小组利用这种思想方法，发现并证明了如下有趣结论，平行四边形两条对角线的平方和等于四边的平方和．请你根据学习小组的思路，完成下列问题：
1. （1） [问题发现]：如图1，学习小组首先通过对特殊平行四边形——矩形（长方形）的研究发现在矩形ABCD中令AB＝a，BC＝b，则可求得AC²+BD²＝；（用a、b的式子表示）
2. （2） [问题探究]：如图2，学习小组通过添加辅助线，尝试将平行四边形转化为矩形，继续对一般平行四边形ABCD进行研究，如图：分别过点A、D作BC边的垂线，请你按照这种思路证明AC²+BD²＝2（AB²+BC²）；
3. （3） [问题拓展]：如图3，在△ABC中，AD是BC边上的中线，已知：AD＝3，BC＝8，（AB-AC）²＝10，请你添加合适的辅助线，构造平行四边形进行转化，求AB•AC的值．
答案解析收藏纠错 + 选题