

已知当电梯乘载的重量超过400千克时警示音响起,且小丽、小欧的重量分别为50千克、70千克.若小丽进入电梯前,电梯内已乘载的重量为千克,则
的取值范围是( )

①与2018年相比,2019年的进口额的年增长率虽然下降,但进口额仍然上升;
②从2018年到2022年,进口额最多的是2022年;
③2018—2022年进口额年增长率持续下降;
④与2021年相比,2022年出口额增加了2.3万亿元





如图,在四边形中,
,
,
,
的角平分线交
于点
, 求证:
.
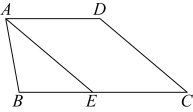
证明:∵平分
,
(已知),
∴( ).
∵(已知),
∴ ▲ ( ).
∵(已知),
∴ ▲ (等量代换).
∴( ).


|
月均用水量频数分布表 |
|
|
分组 |
频数 |
|
|
4 |
|
|
12 |
|
|
|
|
|
9 |
|
|
5 |
|
|
4 |
|
|
2 |
|
合计 |
50 |

请根据图表中提供的信息解答下列问题:
①如图2,当点在点
右侧时,求
与
的数量关系;
②当点在直线
上运动时,
的一边恰好与射线
平行,直接写出此时
的度数(用含
的式子表示).
销售时段 | 销售数量 | 销售收入 | |
A种材质 | B种材质 | ||
第一个月 | 3套 | 5套 | 1800元 |
第二个月 | 4套 | 10套 | 3100元 |

①若 , 求点
的坐标;
②的最小值为;
③动点满足
, 所有动点
组成的图形面积为64,请直接写出
的值.