山西省运城市盐湖区2022-2023学年八年级下学期期末数学...

更新时间：2023-09-09 浏览次数：38 类型：期末考试

一、单选题

1. (2023八下·盐湖期末) 下列多项式能用平方差公式分解因式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·盐湖期末) 剪纸艺术是最古老的中国民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录．鱼与“余”同音，寓意生活富裕，年年有余，是剪纸艺术中很受喜爱的主题．以下关于鱼的剪纸中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023八下·盐湖期末) 如果把 $\text{[math]}$ 中的x和y都变为原来的5倍，那么分式的值（）

A . 变为原来的5倍 B . 不变 C . 变为原来的 $\text{[math]}$ D . 变为原来的4倍

答案解析收藏纠错 + 选题
4. (2023八下·盐湖期末) 若 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·盐湖期末) 已知一个正多边形的每个外角等于45°，则这个正多边形是（）

A . 正五边形 B . 正六边形 C . 正七边形 D . 正八边形

答案解析收藏纠错 + 选题
6. (2023九上·绥阳月考) 将不等式组 $\text{[math]}$ 的解集表示在数轴上正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023八下·盐湖期末) 四边形ABCD的对角线相交于点O，且 $\text{[math]}$ ，那么下列条件不能判断四边形ABCD为平行四边形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·盐湖期末) 如图函数y=2x和y=ax+4的图象相交于A(m，3)，则不等式2x<ax+4的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·盐湖期末) 若 $\text{[math]}$ 是一个完全平方式，则k值是多少？（）

A . 70 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八下·盐湖期末) 如图，已知凸五边形ABCDE的边长均相等，且∠DBE＝∠ABE＋∠CBD，AC＝1，则BD必定满足（）．

A . BD＜2 B . BD＝2 C . BD＞2 D . 以上情况均有可能

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·盐湖期末) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023八下·盐湖期末) x＝时，分式 $\text{[math]}$ 的值为零．

答案解析收藏纠错 + 选题
13. (2023八下·盐湖期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023八下·盐湖期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
15. (2023八下·盐湖期末) 如图，在 $\text{[math]}$ 中，过点B作 $\text{[math]}$ 的平分线 $\text{[math]}$ 的垂线 $\text{[math]}$ ．连接N与 $\text{[math]}$ 中点M，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2023八下·盐湖期末)
1. （1）解不等式组 $\text{[math]}$ ，并求出它的所有整数解的和．
2. （2）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2023八下·盐湖期末) 在解分式方程 $\text{[math]}$ 时，小亮的解法如下：
解：方程两边同时乘 $\text{[math]}$ ，得 $\text{[math]}$ （第一步）
解这个整式方程得： $\text{[math]}$ （第二步）
……
1. （1）任务一：填空
  在上述小亮所解方程中，第步有错，错误的原因是：．
2. （2）任务二：请写出解这个方程的正确过程．
3. （3）任务三：请你根据平时的学习经验，针对解分式方程的注意事项给其他同学再提出一条建议．
答案解析收藏纠错 + 选题
18. (2023八下·盐湖期末) 如图，在平面直角坐标系中， $\text{[math]}$ 三个顶点的坐标分别是 $\text{[math]}$ ．
1. （1）将 $\text{[math]}$ 以点C为旋转中心旋转 $\text{[math]}$ ，画出旋转后对应的 $\text{[math]}$ ；平移 $\text{[math]}$ ，若点A的对应点为点C，画出平移后对应的 $\text{[math]}$ ；
2. （2）若将 $\text{[math]}$ 绕某一点旋转可以得到 $\text{[math]}$ ，请直接写出旋转中心的坐标；
3. （3）在x轴上有一点P，使得 $\text{[math]}$ 值最小，请直接写出点P的坐标．
答案解析收藏纠错 + 选题
19. (2023八下·盐湖期末) 某书店老板去图书批发市场购置某种图书，第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了 $\text{[math]}$ ，他用1500元所购该书的数量比第一次多10本，当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．求该老板在这两次售书中共盈利多少元？

答案解析收藏纠错 + 选题
20. (2023八下·盐湖期末) 已知：如图，在 $\text{[math]}$ 中，点F是 $\text{[math]}$ 上一点，点E是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ．连接 $\text{[math]}$ ，与对角线 $\text{[math]}$ 相交于点O．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

21. (2023八下·盐湖期末) 樱桃是一种常见水果，其中含有丰富的维生素、铁元素、蛋白质、胡萝卜素等营养成分具有补血、抗氧化、健脾益肾的作用，深受人们的喜爱．某水果批发商从水果批发市场批发樱桃进行零售，批发价格与零售价格如下表：

樱桃品种	红灯樱桃	大紫樱桃
批发价（元/kg）	30	50
零售价（元/kg）	55	80

请解答下列问题：

（1）第一天，该经营户批发红灯樱桃和大紫樱桃共 $\text{[math]}$ 用去了10000元，这两种樱桃当天全部销售完一共能赚多少元钱？
（2）第二天，该经营户仍用10000元批发这两种樱桃，要想当天全部售完后所赚钱不少于8100元，则该经营户最少应批发红灯樱桃多少 $\text{[math]}$ ？

答案解析收藏纠错 + 选题

22. (2023八下·盐湖期末) 学完平移与旋转后，数学老师再次介绍了截长补短法：截长补短法是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或者旋转等方式使两条短边拼合到一起，从而解决问题．
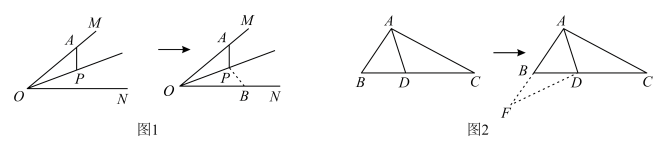
例如：如图1，已知点P是 $\text{[math]}$ 的平分线上一点，点A是射线 $\text{[math]}$ 上任意一点，在 $\text{[math]}$ 上截取B点，使 $\text{[math]}$ （截长法），连接 $\text{[math]}$ ，易得： $\text{[math]}$ ．如图2，已知 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，延长 $\text{[math]}$ 至点F（补短法），使得 $\text{[math]}$ ，连接 $\text{[math]}$ ，易得 $\text{[math]}$ ．
问题情境：
今天我们继续运用截长补短法进行探究学习．如图3，点P是等边 $\text{[math]}$ 外一点，连接 $\text{[math]}$ 且满足 $\text{[math]}$ ，线段 $\text{[math]}$ 之间有何等量关系呢？
经过探究，勤奋小组讲解了他们的思路：
如图4，在 $\text{[math]}$ 上截取一点Q，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．
∵ $\text{[math]}$ 是等边三角形，
∴ $\text{[math]}$ ，
又∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ，
又∵ $\text{[math]}$ ∴ $\text{[math]}$
∴ $\text{[math]}$ （依据1： ▲ ）
∴ $\text{[math]}$ ，
∴ $\text{[math]}$ ，即 $\text{[math]}$
可知 $\text{[math]}$ 是等边三角形（依据2： ▲ ），所以 $\text{[math]}$ ，因此最终得出线段 $\text{[math]}$ 之间的等量关系是 ▲ ．
1. （1）反思交流：
  ①上述证明过程中“依据1”“依据2”分别指什么？
  依据1：．
  依据2：．
  ②图3中线段 $\text{[math]}$ 之间的等量关系是．
2. （2）探索发现：
  创新小组受勤奋小组的启发，把点D移动到边 $\text{[math]}$ 下方，如图5， $\text{[math]}$ 是等边三角形，且点D是边 $\text{[math]}$ 下方一点， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，根据上述解题思路，继续探究三条线段 $\text{[math]}$ 之间的等量关系，并写出你的证明过程．
3. （3）问题解决：
  请你参考上面的解题思路，探究并解决下列问题：如图6，在正方形 $\text{[math]}$ 内有一点P，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ ＝．
答案解析收藏纠错 + 选题
23. (2023八下·盐湖期末) 【综合探究】已知 $\text{[math]}$ 在平面直角坐标系中的位置如图所示，其中边 $\text{[math]}$ 在 $\text{[math]}$ 轴上且 $\text{[math]}$ ，边 $\text{[math]}$ 在 $\text{[math]}$ 轴上且 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）请直接写出 $\text{[math]}$ 、 $\text{[math]}$ 两点的坐标： $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）如图1，求点 $\text{[math]}$ 的坐标．
3. （3）过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．如图2，求 $\text{[math]}$ 面积．
4. （4）在平面内是否存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四点组成的四边形是平行四边形，若存在，请直接写出点 $\text{[math]}$ 的坐标：若不存在，请说明理由．
答案解析收藏纠错 + 选题