一、选择题（本题共10小题，每小题2分，共20分，在每小题给出的四个选项中，只有一个选项正确）
-
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
-
A . 1
B . －1
C . 2
D . －2
-
A . 1和2之间
B . 2和3之间
C . 3和4之间
D . 4和5之间
-
-
A . 100°
B . 120°
C . 130°
D . 140°
-
8.
(2023七下·大连期末)
一件商品的进货价是100元，如果按原售价的八折销售，至少可获得10%的利润，若设该商品的原售价是
x元，则列式正确的是（ ）
-
9.
(2023七下·大连期末)
某校为了解七年级900名学生在本次体育测试的成绩情况，现随机抽取若干名学生的体育测试成绩进行统计，并绘制了如下两幅统计图．
则下列结论不正确的是（ ）
A . 本次抽样调查的样本容量是100
B . 体育测试成绩在40分以下占抽取人数的10%
C . 在扇形统计图中，体育测试成绩为50分所在扇形的圆心角为90°
D . 若把体育成绩在45分以上（含45分）定为合格，则全校七年级学生体育成绩合格人数约630人
-
二、填空题（本题共6小题，每小题3分，共18分）
-
-
-
-
14.
(2023七下·大连期末)
《九章算术》是中国古代第一部数学专著，书中有这样一题：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何?”大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人?该物品价格是多少?设共有
x个人，该物品价格是
y元，则可列方程组为
．
-
15.
(2024八上·涪城开学考)
某工程队计划在5天内修路6km，施工第一天修完1.2km，计划发生变化，需至少提前1天完成修路任务，则后期每天至少修路
千米．
-
16.
(2023七下·大连期末)
如图，在平面直角坐标系中，一动点从原点
O出发，沿着箭头所示方向，每次移动1个单位长度，依次得到点
，
，
，
，
，
， …，则点
的坐标是
．
三、解答题（本题共4小题，其中17题6分，18、19、20题各8分，共30分）
-
-
-
19.
(2023七下·大连期末)
如图，在三角形
ABC中，点
D在
BC上，连接
AD ， 点
E、
F分别在
AD、
AB上，连接
DF ， 且∠
DFE＝∠
C ， ∠1＋∠2＝180°．求证：∠
CAB＝∠
DFB ．
请完善解答过程，并在括号内填写相应的理论依据．
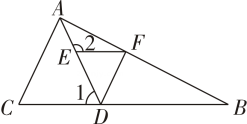
证明：∵∠1＋∠2＝180°（已知），∵∠DEF＋∠2＝180°（邻补角的定义），
∴∠1＝∠DEF（ ），
∴
（ ），
∴∠DFE＝∠BDF（ ），
又∵∠DFE＝∠C（已知），∴∠BDF＝ ▲ （ ），
∴
▲ （ ），
∴∠CAB＝∠DFB（ ）．
-
20.
(2023七下·大连期末)
为了解某区初中生每周锻炼身体的时长s（单位：小时）的情况，在全区随机抽取部分初中生进行调查，按五个组别：A组（3≤t＜4），B组（4≤t＜5），C组（5≤t＜6），D组（6≤t＜7），E组（7≤t＜8）进行整理，绘制如下两幅不完整的统计图．
所抽取学生每周锻炼时长的扇形统计图所抽取学生每周锻炼时长的频数直方图
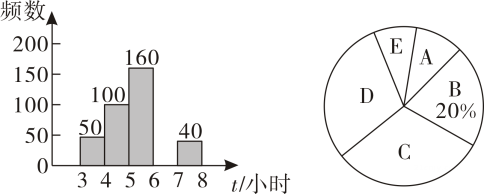
根据图中提供的信息，解决下列问题：
-
（1）
本次抽样调查了名学生，其中D组（6≤t＜7）有名学生，A组（3≤t＜4）所在的扇形圆心角为°；
-
（2）
根据抽样调查结果，请你估计该区5000名初中生中锻炼时长不少于6小时的学生人数．
四、解答题（本题共2小题，其中21题8分，22题10分，共18分）
-
21.
(2023七下·大连期末)
如图，这是某市部分简图，小正方形网格的单位长度为1．
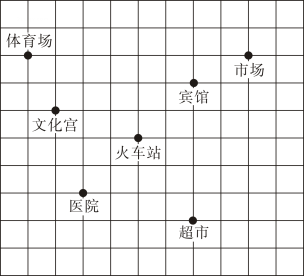
⑴请你以火车站为原点建立平面直角坐标系；
⑵直接写出医院的坐标为 ；
⑶将体育场、宾馆分别记作点A ， 点B ， 连接AB ， 将线段AB向右平移1个单位长度，再向下平移4个单位长度，得到线段
（点A的对应点为点
， 点B的对应点为点
），画出线段 ， 并直接写出点和点的坐标．
-
22.
(2023七下·大连期末)
某校计划购买
A型和
B型两种笔记本作为奖品发放给学生，若购买
A型笔记本3本，
B型笔记本4本，共需44元；若购买
A型笔记本6本，
B型笔记本2本，共需58元．
-
-
（2）
该校计划购买A型和B型两种笔记本共60本，费用不超过400元，A型笔记本最多买多少本?
五、解答题（本题共2小题，其中23题10分，24题12分，共22分）
-
23.
(2023七下·大连期末)
据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊讶，忙问计算的奥秘．你知道华罗庚是怎样迅速准确地计算出来的吗?请按照下面的问题试一试：
-
（1）
由
，
， 可以确定
是
位数，由59319的个位上的数是9，可以确定
的个位上的数字是
，如果划去59319后面的三位319得到数59，而
，
， 由此可以确定
的十位上的数字是
；
-
（2）
已知32768，－274625都是整数的立方，按照上述方法，请你分别求它们的立方根．
-
-
-
（2）
如图2．
， ∠
GEH＝
n∠
AEH ， ∠
EHF＝30°，求
n的值；
-
（3）
如图3，延长EG交CD于点K ， 点M在射线KF上（点M不与点K ， F重合），EN平分MEF ， 画出图形，写出∠KEN与∠EMF之间的数量关系，并说明理由．
六、解答题（本题12分）
-
-
-
（2）
将线段AB向左平移2个单位得到线段CD（点A的对应点为点C ， 点B的对应点为点D），线段CD与y轴交于点E ， 求点E的坐标；
-
（3）
点M为（2）中直线CD上一动点，连接BC ， BM ， 设点M的横坐标为m ， 三角形MBC的面积为S ， 当8≤S≤10时，求m的取值范围．
