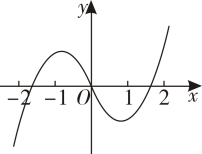
 B .
B . 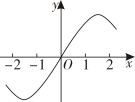 C .
C . 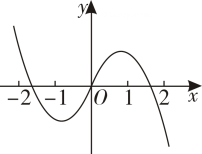 D .
D . 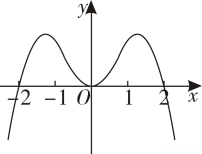
天干:甲 乙 丙 丁 戊 己 庚 辛 壬 癸
地支:子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
把天干与地支按以下方法依次配对:把第一个天干“甲”与第一个地支“子”配出“甲子”,把第二个天干“乙”与第二个地支“丑”配出“乙丑”, , 若天干用完,则再从第一个天干开始循环使用.已知2023年是癸卯年,则
年以后是年.
| 集齐“五福”卡 | 末集齐“五福”卡 | 合计 |
男性 | 80 | 20 | 100 |
女性 | 65 | 35 | 100 |
合计 | 145 | 55 | 200 |
参考公式: , 其中
.
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
喜爱 | 不喜爱 | |
A类体操 | 70 | 30 |
B类体操 | 40 | 60 |
附: ,