北京市北大附中2023届高三下学期三模物理试题

更新时间：2023-11-23 浏览次数：54 类型：高考模拟

一、本部分共14题，每题3分，共42分。在每题列出的四个选项中，选出最符合题目要求的一项。

1. (2023高三下·北京市模拟) 下列有关热现象的叙述中正确的是（　　）

A . 分子间的作用力随分子间距离的增大而减小 B . 分子势能一定随分子间距离的增大而增大 C . 温度升高，每个分子的动能都增大 D . 粗测分子直径可利用“油膜法”，测量单分子油膜的厚度可认为是分子直径

答案解析收藏纠错 + 选题
2. (2023高三下·北京市模拟) 一束复色可见光射到置于空气中的平板玻璃上，穿过玻璃后从下表面射出，变为a、b两束平行单色光，如图所示。对于两束单色光来说（　　）

A . 玻璃对a光的折射率较小 B . a光在玻璃中传播的速度较大 C . b光的波长较长 D . b光光子的能量较大

答案解析收藏纠错 + 选题
3. (2023高三下·北京市模拟) 下列与 $\text{[math]}$ 粒子相关的说法中正确的是（　　）

A . $\text{[math]}$ （铀238）核放出一个 $\text{[math]}$ 粒子后就变为 $\text{[math]}$ （钍234） B . 天然放射性现象中产生的 $\text{[math]}$ 射线速度与光速相当，贯穿能力很强 C . 高速 $\text{[math]}$ 粒子轰击氮核可从氮核中打出中子，核反应方程为 $\text{[math]}$ D . 丹麦物理学家玻尔进行了 $\text{[math]}$ 粒子散射实验并首先提出了原子的核式结构模型

答案解析收藏纠错 + 选题
4. (2023高三下·北京市模拟) 一列简谐横波某时刻的波形图如图甲表示，图乙表示介质中某质点此后一段时间内的振动图像，则下列说法正确的是

A . 若波沿x轴正向传播，则图乙表示P点的振动图像 B . 若图乙表示Q点的振动图像，则波沿x轴正向传播 C . 若波速是20m/s，则图乙的周期是0.02s D . 若图乙的频率是20Hz，则波速是10m/s

答案解析收藏纠错 + 选题
5. (2023高三下·北京市模拟) 2017年4月7日出现了“木星冲日”的天文奇观，木星离地球最近最亮．当地球位于太阳和木星之间且三者几乎排成一条直线时，天文学称之为“木星冲日”．木星与地球几乎在同一平面内沿同一方向绕太阳近似做匀速圆周运动．不考虑木星与地球的自转，相关数据见下表．则（）
质量半径与太阳间距离
地球 m R r
木星约320m 约11R 约5r

A . 木星运行的加速度比地球运行的加速度大 B . 木星表面的重力加速度比地球表面的重力加速度大 C . 下一次“木星冲日”的时间大约在2027年7月份 D . 在木星表面附近发射飞行器的速度至少为7.9km/s

答案解析收藏纠错 + 选题
6. (2023高二上·上海市月考) 安培对物质具有磁性的解释可以用如图所示的情景来表示，那么（　　）

A . 甲图代表了被磁化的铁棒的内部情况 B . 乙图代表了被磁化的铁棒的内部情况 C . 磁体在高温环境下磁性不会改变 D . 磁体在高温环境下磁性会加强

答案解析收藏纠错 + 选题
7. (2023高三下·北京市模拟) 正弦交变电源与电阻R、交流电压表按照图1所示的方式连接， $\text{[math]}$ ，交流电压表的示数是 $\text{[math]}$ ，图2是交变电源输出电压u随时间t变化的图像。则（　　）

A . 通过R的电流 $\text{[math]}$ 随时间t变化的规律是 $\text{[math]}$ B . 通过R的电流最大值是 $\text{[math]}$ C . R两端的电压 $\text{[math]}$ 随时间t变化的规律是 $\text{[math]}$ D . R两端的电压有效值是 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三下·北京市模拟) 一质量为 $\text{[math]}$ 的物块在水平力F的作用下由静止开始在水平地面上做直线运动。F随时间t变化的图线如图所示，已知物块与地面间的动摩擦因数为 $\text{[math]}$ ，重力加速度g取 $\text{[math]}$ 。则（　　）

A . $\text{[math]}$ 时物块的动量大小为 $\text{[math]}$ B . $\text{[math]}$ 时物块的速度大小为 $\text{[math]}$ ，方向向右 C . $\text{[math]}$ 时间内F对物块的冲量大小为 $\text{[math]}$ D . $\text{[math]}$ 时间内物体的位移为 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023高三下·北京市模拟) 复兴号动车在世界上首次实现速度350km/h自动驾驶功能，成为我国高铁自主创新的又一重大标志性成果。一列质量为m的动车从静止开始以恒定功率P在平直轨道上运动，经时间t达到该功率下的最大速度 $\text{[math]}$ ，设动车行驶过程所受到的阻力F保持不变。动车在时间t内（）

A . 牵引力保持不变 B . 加速度逐渐变大 C . 牵引力的功率 $\text{[math]}$ D . 牵引力做功 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高三下·北京市模拟) 如图所示，有两个静止的带等量正电的点电荷，分别放置在M、N两点，在M、N连线上有O、a、c三点，其中O点是连线的中点，a、c关于O点对称，在M、N连线的中垂线上还有对称的b、d两点，则下列说法正确的是（　　）

A . a、c两点处场强相同，b、d两点处场强相同 B . a、c两点处电势不相等，b、d两点处电势相等 C . 某负点电荷在c点的电势能大于在d点的电势能 D . 在b点静止释放一负点电荷（不计重力）将在 $\text{[math]}$ 之间往复运动

答案解析收藏纠错 + 选题
11. (2023高三下·北京市模拟) 1831年8月，法拉第在软铁环两侧分别绕有M、N两个线圈的实验中，发现了电磁感应现象。装置如图所示，在正确操作的情况下，符合实验事实的选项是（　　）

A . 闭合开关瞬间，电流计指针无偏转 B . 闭合开关稳定后，电流计指针有偏转 C . 开关断开的瞬间，感应电流的方向为a→电流计→b D . 将绕线的铁环换成木环，闭合开关瞬间，电流计指针会明显偏转

答案解析收藏纠错 + 选题
12. (2023高三下·北京市模拟) 磁电式电流表是常用的电学实验器材。如图所示，电表内部由线圈、磁铁极靴、圆柱形.软铁螺旋弹簧等构成。下列说法正确的是（　　）

A . 极靴与圆柱形软铁之间为匀强磁场. B . 当线圈中电流方向改变时，线圈受到的安培力方向不变 C . 通电线圈通常绕在铝框上，主要因为铝的电阻率小，可以减小焦耳热的产生 D . 在运输时.通常把正、负极接线柱用导线连在一起，是应用了电磁阻尼的原理

答案解析收藏纠错 + 选题
13. (2023高三下·北京市模拟) 据统计交通事故逐年增加，造成交通事故的一个主要原因就是酒后驾驶，“严查酒驾”成为全国交通部门的一项重要任务。酒精测试仪是用于现场检测机动车驾驶人员是否酗酒的一种仪器，它的主要元件是由二氧化锡半导体制成的酒精气体传感器，该传感器的电阻随酒精气体浓度的变化而变化。在如图所示的电路中，不同的酒精气体浓度对应着传感器的不同电阻，这样，显示仪表的指针就与酒精气体浓度有了对应关系。如果二氧化锡半导体型酒精气体传感器电阻r′的倒数与酒精气体的浓度c成正比，则以下说法正确的是（　　）

A . U越大，表示c越小 B . U越大，表示c越大 C . 检测到驾驶员喝了酒时，U的示数变小 D . U越大，表示检测到驾驶员喝酒越少

答案解析收藏纠错 + 选题
14. (2023高三下·北京市模拟) 2019年4月10日，人类史上首张黑洞照片发布，照片中是室女座巨椭圆星系M87的黑洞照片，这是黑洞存在最直接的视觉证据．黑洞最初是一个衰老的巨大恒星，它的质量要达到太阳的数十倍以上，恒星不断的发光发热，随着恒星中心的“燃料”不断消耗，恒星内部能量不足，无法支撑外壳重压，恒星内核开始塌缩．最终，所有物质缩成一个体积接近无限小的点，这便是奇点．奇点会形成强大引力场，吸收周围物质，就连光也会被吸进去，至此黑洞诞生．拍摄黑洞用的是事件视界望远镜，该望远镜收集到的不是我们日常的可见光，而是一种波长比光波更长的亚毫米波，亚毫米波本身是没有颜色的区别，科学家们实际上只能感受到强弱的不同．发布的图片中心黑暗区域正中为黑洞．周围环绕一个新月状光环，一侧亮一些，另一侧暗一些，是因为光环旋转，导致接收者接收到相位和频率变化造成的．根据以上信息下列说法正确的是

A . 恒星发光发热是恒星内部的核裂变造成的 B . 环状新月型光环上下两侧不对称是多普勒效应造成的 C . 黑洞的第一宇宙速度是光速 D . 事件视界望远镜收集的亚毫米波比可见光的频率大

答案解析收藏纠错 + 选题

二、第二部分

15. (2023高三下·北京市模拟) 物理实验一般都涉及实验目的、实验原理、实验仪器、实验方法、实验操作、数据分析等。
1. （1）如图1所示，在“探究影响感应电流方向的因素”实验中，下列实验操作中说法正确的是____。
  
  A . 判断感应电流的方向时，需要先确定线圈的绕向 B . 实验中将条形磁铁快速插入或快速拔出时，指针偏转将更加明显 C . 实验中将条形磁铁插入时，插入快慢对实验现象不产生影响 D . 将条形磁铁N极向下插入线圈或S极向下插入线圈，电流表的偏转方向相同
2. （2）在“利用单摆测重力加速度”的实验中
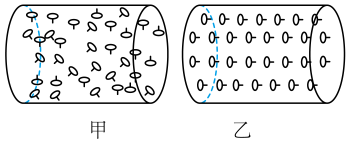
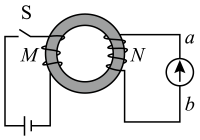
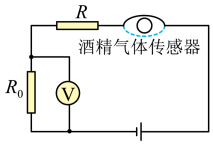
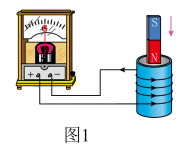
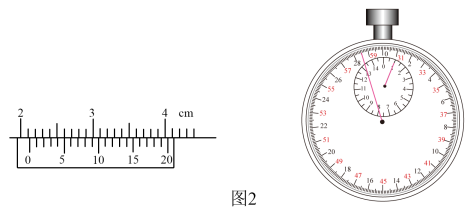
  ①如图2所示，某同学先用游标卡尺测量单摆1的摆球直径为mm，然后用秒表记录了此单摆振动30次所用的时间为s。
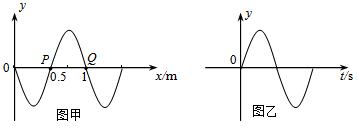
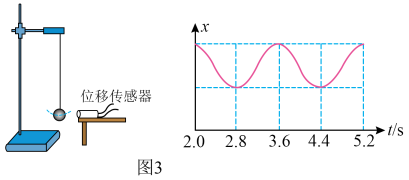
  ②另一同学将单摆2固定在铁架台上，使其做小角摆动（摆动路径如图中虚线所示），通过位移传感器得到了摆球位移随时间的变化曲线，已知摆长 $\text{[math]}$ ，根据图3中的信息可得，重力加速度 $\text{[math]}$ $\text{[math]}$ （结果保留两位有效数字， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
16. (2023高三下·北京市模拟) 如图所示，甲同学用半径相同的A、B两球的碰撞可以验证“动量守恒定律”。实验时先让质量为 $\text{[math]}$ 的A球从斜槽轨道上某一固定位置S由静止开始滚下，从轨道末端抛出，落到位于水平地面的复写纸上，在下面的白纸上留下痕迹。重复上述操作10次，得到10个落点痕迹，P为落点的平均位置。再把质量为 $\text{[math]}$ （ $\text{[math]}$ ）的B球放在斜槽轨道末端，让A球仍从位置S由静止滚下，与B球碰撞后，分别在白纸上留下各自的落点痕迹，重复操作10次，M、N分别为落点的平均位置。
1. （1）实验中，直接测定小球碰撞前后的速度是不容易的。但是，可以通过仅测量____间接地解决这个问题。
  
  A . 小球开始释放高度h B . 小球抛出点距地面的高度H C . 小球做平抛运动的射程 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$
2. （2）以下提供的测量工具中，本实验必须使用的是____。
  
  A . 刻度尺 B . 天平 C . 游标卡尺 D . 秒表
3. （3）关于本实验，下列说法正确的是____。
  
  A . 斜槽轨道必须光滑 B . 斜槽轨道末端必须水平 C . 实验过程中，复写纸可以移动
4. （4）在实验误差允许范围内，若满足关系式，则可以，则可以认为两球碰撞为弹性碰撞。（用已知量和（1）中测得的物理量表示）
5. （5）乙同学想借助如图所示的水平气垫导轨验证动量守恒定律。水平气垫导轨（接通电源后，导轨与滑块间摩擦力忽略不计）上装有两个光电门计时装置，可以记录遮光片的遮光时间，导轨上还配有两个带遮光片的滑块A、B，两个遮光片的规格完全相同。除此之外，实验室可供使用的实验器材有一台天平、一根轻弹簧，请通过分析说明该同学能否完成验证。若能，请简要说明实验操作过程，并写出需要测量的物理量及这些物理量应满足的关系式；若不能，请说明理由并给出需要补充的实验器材清单。
答案解析收藏纠错 + 选题
17. (2023高三下·北京市模拟) 如图所示，把一个质量m₁=0.2kg的小球放在高度为h=5.0m的直杆的顶端。一颗质量m′=0.01kg的子弹以v₀=500m/s的速度沿水平方向击中小球，并穿过球心，小球落地处离杆的距离为s=20m。g取10m/s² ，求：
1. （1）子弹穿过小球时，小球的速度；
2. （2）子弹落地处离杆的距离sʹ；
3. （3）子弹击穿小球的过程中，子弹与小球系统损失的机械能。
答案解析收藏纠错 + 选题
18. (2023高三下·北京市模拟) 如图所示，两根平行光滑金属导轨 $\text{[math]}$ 和 $\text{[math]}$ 放置在水平面内，其间距为L，磁感应强度为B的匀强磁场垂直轨道平面向下，两导轨之间连接电阻R，在导轨上有一金属棒 $\text{[math]}$ ，其电阻为r，金属棒与导轨垂直且接触良好。在 $\text{[math]}$ 棒上施加水平拉力使其以速度v向右匀速运动，设金属导轨足够长。求：
1. （1）请根据法拉第电磁感应定律推导出闭合电路的感应电动势 $\text{[math]}$ ；
2. （2）金属棒a、b两点间的电势差；
3. （3）时间t内电阻R产生的焦耳热。
答案解析收藏纠错 + 选题
19. (2023高三下·北京市模拟) 如图所示为离子发动机的示意图：其原理是设法将惰性气体（比如氙气）电离，使中性的原子变成带正电的离子，这些带正电的气体离子经过加速电场加速，以很高的速度沿同一方向喷出舱室，由此产生推力。由于单位时间内喷出的气体离子质量很小，探测器得到的加速度会非常小，但经过足够长时间的加速，同样可以得到很大的速度。假如探测器连同离子发动机和氙气的总质量为M，每个氙离子的质量为m，电量为q，加速电压为U，离子加速后形成的电流强度为I，为研究问题方便，假定离子推进器在太空中飞行时不受其它外力，忽略推进器运动速度，求：
1. （1）发动机单位时间内喷出多少个氙离子；
2. （2）离子发动机工作的初始阶段，产生推力能使探测器产生的加速度大小；
3. （3）为使离子推进器正常运行，必须在有离子喷射的出口处用中和电子枪向正离子喷射电子，试解释其原因。
答案解析收藏纠错 + 选题
20. (2023高三下·北京市模拟) 中国国家跳水队是中国体育届的王牌之师，自1984年首次参加洛杉矶奥运会以来，已为中国体育代表团累计贡献了40枚奥运金牌，在各项奥运项目中高居榜首，被誉为跳水“梦之队”，在第32届东京奥运会中，他们也取得了7金5银的骄人战绩。有位同学对跳水中的物理问题很感兴趣，打算利用频闪照相技术详细研究跳水的过程。在下面的问题中，空气阻力均可忽略，重力加速度取 $\text{[math]}$ 。
1. （1）该同学在研究某运动员高台跳水过程的频闪照片时，观察到该运动员从离水面 $\text{[math]}$ 高的平台向上跃起，到达最高点后近似竖直下落直至入水。该同学将照片放大进行观察，发现照片中的最后一个影像恰好为入水前一瞬间，由于运动员的运动，这一影像上下错开的距离约为 $\text{[math]}$ 。已知相机单次曝光时间为 $\text{[math]}$ ，实际高为 $\text{[math]}$ 的跳台在照片中高 $\text{[math]}$ ，试估算运动员的重心在最高点时相较入水前一刻的高度。
2. （2）运动员入水时往往是头部朝下，身体竖直且呈绷直状态，从运动员指尖触碰到水面到脚尖刚好完全进入水里的入水过程中，可以将人体简化为一竖直方向的均匀实心圆柱，并且只考虑人的重力和水的浮力对人的作用（即忽略水的阻力）。请通过推导证明运动员在入水过程中的运动性质是简谐运动，可以认为水的密度略大于人的密度。（注意：在解题过程中需要用到，但题目没有给出的物理量，需要在解题时做必要说明）
3. （3）除了跳台跳水外，跳板跳水是另一种常见的跳水方式。某同学通过上网查阅资料，了解到了跳水板的相关信息如下表所示：
  名称
  材质
  规格型号
  跳水板
  航空级铝合金（6070-T6）
  重量 $\text{[math]}$
  尺寸 $\text{[math]}$
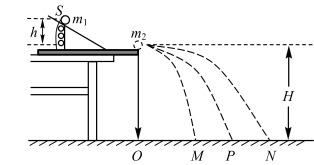
  他考虑到跳板跳水在起跳过程中借助了跳板的弹性，可能更容易获得较高的腾空高度，因此利用频闪照相记录了某位运动员在3米跳板比赛中的全过程，如图所示。
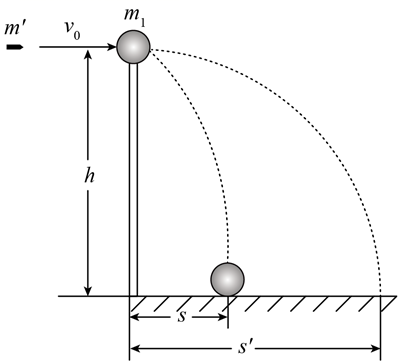
  a、在进行分析时，该同学把运动员看作一个质点，将跳板简化为一个竖直放置的轻弹簧，弹力大小F与形变量x之间的关系为 $\text{[math]}$ （已知相应的弹性势能为 $\text{[math]}$ ），其中k为常量。质量为 $\text{[math]}$ 的运动员静止站在跳板末端时，末端相比跳板在自由状态时下降了 $\text{[math]}$ ，之后，运动员通过自身做功将跳板末端压到最大形变量为 $\text{[math]}$ 后起跳，忽略该过程中的机械能损失，请计算该运动员的最大理论腾空高度H（即离开板面后重心上升的高度）和该过程需要做的功W。
  b、请你评价该同学在（a）中的建模过程是否合理。如果认为合理，请通过计算比较在同等做功情况下跳台跳水和跳板跳水的最大腾空高度；如果认为不合理，请指出其存在的问题，并针对“估算最大腾空高度”的建模过程给出较为合理的分析思路。
答案解析收藏纠错 + 选题