浙江省杭州市西湖区丰潭中学2023年中考二模数学试卷

更新时间：2023-10-24 浏览次数：221 类型：中考模拟

一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2023·杭州模拟) 下列计算结果为5的是（）

A . -（+5） B . +（-5） C . -（-5） D . -|-5|

答案解析收藏纠错 + 选题
2. (2023·杭州模拟) 杭州亚运会赛会志愿者招募自启动以来，得到了社会群体和高校学生的积极响应，注册总人数超32万人．其中32万用科学记数法可表示为（）

A . 32×10⁴ B . 3.2×10⁵ C . 3.2×10⁶ D . 0.32×10⁶

答案解析收藏纠错 + 选题
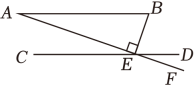
3. (2023·杭州模拟) 如图，AB∥CD ， AF交CD于点E ， ∠B＝70°，则∠DEF的度数是（）

A . 10° B . 20° C . 30° D . 40°

答案解析收藏纠错 + 选题
4. (2023·杭州模拟) 若x+3＜0，则下列各式中正确的是（）

A . x+1＞0 B . x-1＞0 C . $\text{[math]}$ D . -2x＞6

答案解析收藏纠错 + 选题
5. (2023·杭州模拟) 分析一组数据时，圆圆列出了方差的计算公式S²＝ $\text{[math]}$ 由公式提供的信息，可得出n的值是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2023·杭州模拟) 某商铺促销，单价80元的衬衫按照8折销售仍可获利10元，若这款衬衫的成本价为x元/件，则（）

A . 80×0.8-x＝10 B . （80-x）0.8-x＝10 C . 80×0.8＝x-10 D . （80-x）×0.8＝x-10

答案解析收藏纠错 + 选题
7. (2023·杭州模拟) 在平面直角坐标系中，点A（a ， a²-1）在第二象限内，则a的取值可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·杭州模拟) 如图，正九边形外接圆的半径是R，则这个正九边形的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·杭州模拟) 如图，点O为△ABC的内心，∠B＝60°，点M，N分别为AB，且OM＝ON．甲、乙两人有如下判断：甲：∠MON＝120°：乙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（）

A . 只有甲正确 B . 只有乙正确 C . 甲、乙都正确 D . 甲、乙都错误

答案解析收藏纠错 + 选题
10. (2023·杭州模拟) 已知二次函数y＝ax²+bx+c，当y＞n时，x的取值范围是m-3＜x＜1-m，且该二次函数的图象经过点P（3，t²+5），Q（d，4t）两点，则d的值可能是（）

A . 0 B . -1 C . -4 D . -6

答案解析收藏纠错 + 选题

二、填空题：本大题有6个小题，每小题4分，共24分.

11. (2024八上·斗门期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2024八下·本溪期中) 分解因式：a²﹣2ab=

答案解析收藏纠错 + 选题
13. (2023·杭州模拟) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个解．

答案解析收藏纠错 + 选题
14. (2023·杭州模拟) 已知扇形的半径为3cm ，圆心角为150°，则该扇形的弧长为cm ．

答案解析收藏纠错 + 选题
15. (2023·杭州模拟) 如图，正六边形ABCDEF的边长为2cm，点P是线段BF上一点，则阴影部分的面积为cm²

答案解析收藏纠错 + 选题
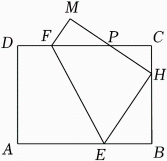
16. (2023·杭州模拟) 如图，一张矩形纸片ABCD中， $\text{[math]}$ （m为常数），将矩形纸片ABCD沿EF折叠，点D的对应点为点M ， CD与HM交于点P ．当点H落在BC的中点时，且 $\text{[math]}$ ， m=．

答案解析收藏纠错 + 选题

三、解答题：本大题有7个小题，共66分，解答应写出文字说明、证明过程或演算步骤.

17. (2023·杭州模拟) 先化简： $\text{[math]}$ ，再从-2＜x≤2中选出一个合适的x的整数值代入求值．

答案解析收藏纠错 + 选题
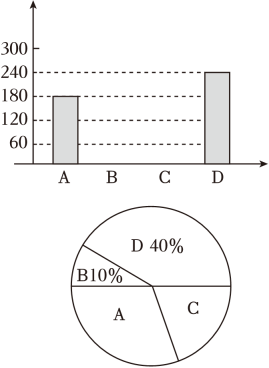
18. (2023·杭州模拟) 端午节是中国的传统节日．今年端午节前夕，杭州市某食品厂抽样调查了某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况，并将调查情况绘制成如图两幅不完整统计图：
1. （1）根据题中信息补全条形统计图，并求出喜欢C种口味粽子的人数所占圆心角为度．
2. （2）若有外型完全相同的A、B、C、D四种不同口味的粽子各一个，煮熟后，小李吃了两个，求出小李第二个吃的粽子恰好是A种粽子的概率．
答案解析收藏纠错 + 选题
19. (2023·杭州模拟) 如图，在△ABC中，AB＝AC ，以CB ， CD为边作▱DCBE
1. （1）若∠A＝50°，求∠E的度数．
2. （2）若AD＝3CD ， BC＝6，求EF ．
答案解析收藏纠错 + 选题
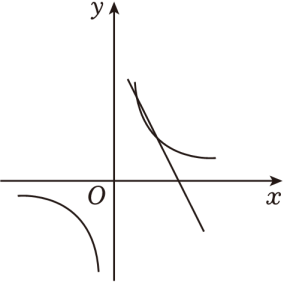
20. (2023·杭州模拟) 设函数 $\text{[math]}$ （k＞0，k是常数），函数y₂＝-2x+7的图象交于点P（a₁ ， b₁），点Q（a₂ ， b₂）．
1. （1）当a₁＝2时，求k的值．
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
3. （3）若2＜x＜3时，总有y₁＜y₂ ，求k的取值范围．
答案解析收藏纠错 + 选题
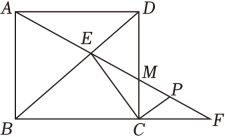
21. (2023·杭州模拟) 如图，已知正方形ABCD ， AB＝4，射线AM交BD于点E ，交射线BC于点F ，交AF于点P ．
1. （1）求证：△ADE≌△CDE ．
2. （2）判断△CPF的形状，并说明理由．
3. （3）作DM的中点N ，连结PN ，若PN＝3
答案解析收藏纠错 + 选题
22. (2023·杭州模拟) 已知二次函数y＝x²-4x的图象经过A（x₁ ， t），B（x₂ ， t），C（m ， n）三点，且x₁＜x₂ ．
1. （1）当t＝5时，求点A和点B的坐标；
2. （2）将点C先向右平移1个单位长度，再向下平移2个单位长度，得点D ，求n的值；
3. （3）当a≤m≤5时，n的最大值为5，n的最小值是-4
答案解析收藏纠错 + 选题
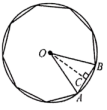
23. (2023·杭州模拟) 如图，AB ， CD是⊙O的两条直径，点E是 $\text{[math]}$ 上一动点（点E不与B ， D重合），CE ，分别交OD ， G ，连接AC ．设⊙O的半径为r ， ∠OAF＝α．
1. （1） ∠OCG＝（用含α的代数式表示）；
2. （2）当α＝30°时，求证：AF＝2FE；
3. （3）判断AG•CF是否为定值．若是，求出该定值；若不是
答案解析收藏纠错 + 选题