
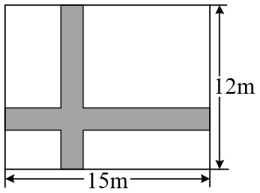

|
|
… |
|
|
|
|
|
… |
|
|
… |
|
|
|
|
|
… |
|
|
… |
|
|
|
|
|
… |
(参考数据:)
请用含字母的算式表示以上算式的一般特征: .
如果 , 其中
均为整数,则
的取值有( )
.1个
.2个
.3个
.4个
若 , 则
▲ ,
▲ .
请运用这个思路和幂的运算法则解决下列问题:
根据平方根的定义可得:∵ , ∴
.
根据平方根的定义可得:∵是
的一个平方根,∴
.
根据平方根的定义,利用上述符号及例子解决下列问题:
;
.
证明:∵是
的平方根,
∴ .
∵(依据
)
, (依据
)
∴ .
填写推理依据,
依据: ▲ ;
依据: ▲ .
计算:
.