浙江省温州市乐清市重点中学2023-2024学年高二上册数学...

更新时间：2023-11-10 浏览次数：44 类型：开学考试

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2023高二上·乐清开学考) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高二上·乐清开学考) 在平面直角坐标系 $\text{[math]}$ 中，动点 $\text{[math]}$ 的坐标满足方程 $\text{[math]}$ ，则点 $\text{[math]}$ 的轨迹经过（）

A . 第一、二象限 B . 第二、三象限 C . 第三、四象限 D . 第一、四象限

答案解析收藏纠错 + 选题
3. (2023高二上·乐清开学考) 要得到余弦曲线 $\text{[math]}$ ，只需将正弦曲线 $\text{[math]}$ 向左平移（）

A . $\text{[math]}$ 个单位 B . $\text{[math]}$ 个单位 C . $\text{[math]}$ 个单位 D . $\text{[math]}$ 个单位

答案解析收藏纠错 + 选题
4. (2023高二上·乐清开学考) 设直线 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 的（）

A . 充要条件 B . 必要不充分条件 C . 充分不必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
5. (2023高二上·乐清开学考) 已知圆 $\text{[math]}$ ，圆 $\text{[math]}$ ，则圆C₁与圆C₂的位置关系是（）

A . 内含 B . 外离 C . 相交 D . 相切

答案解析收藏纠错 + 选题
6. (2023高二上·乐清开学考) 设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则a ， b ， c的大小关系为（）

A . c＜b＜a B . c＜a＜b C . b＜a＜c D . b＜c＜a

答案解析收藏纠错 + 选题
7. (2023高二上·乐清开学考) 在 $\text{[math]}$ 中，已知 $\text{[math]}$ 是 $\text{[math]}$ 边上的中点， $\text{[math]}$ 是 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则实数 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
8. (2023高二上·乐清开学考) 如图，正方体 $\text{[math]}$ 的棱长为1，正方形 $\text{[math]}$ 的中心为O ，棱 $\text{[math]}$ ， $\text{[math]}$ 的中点分别为E ， F ，则下列选项中不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 点F到直线 $\text{[math]}$ 的距离为 $\text{[math]}$ D . 异面直线 $\text{[math]}$ 与 $\text{[math]}$ 所成角的余弦值为 $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题（本大题共4小题，每小题5分，共计20分.在每小题给出的四个选项中，有多项符合题目求，全部选对的得5分，有选错的得0分，部分选对的得2分）

9. (2023高二上·乐清开学考) 在空间中，设 $\text{[math]}$ 为两条不同的直线， $\text{[math]}$ ， $\text{[math]}$ 为两个不同的平面，则下列正确的是（）

A . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·乐清开学考) 下列说法正确的是（）

A . 直线 $\text{[math]}$ 的倾斜角的取值范围为 $\text{[math]}$ B . “ $\text{[math]}$ ”是“点 $\text{[math]}$ 到直线 $\text{[math]}$ 距离为3”的充要条件 C . 直线 $\text{[math]}$ 恒过定点 $\text{[math]}$ D . 直线 $\text{[math]}$ 与直线 $\text{[math]}$ 垂直，且 $\text{[math]}$ 与圆 $\text{[math]}$ 相交

答案解析收藏纠错 + 选题
11. (2023高二上·乐清开学考) 已知正数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高二上·乐清开学考) 已知函数 $\text{[math]}$ ，若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两解，则实数 $\text{[math]}$ 的值可能为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：（本题共4小题，每小题5分，共20分.）

13. (2023高二上·乐清开学考) 若复数 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023高二上·乐清开学考) 若两条直线 $\text{[math]}$ 与 $\text{[math]}$ 平行，则 $\text{[math]}$ 与 $\text{[math]}$ 间的距离是.

答案解析收藏纠错 + 选题
15. (2023高二上·乐清开学考) 一个三位自然数，百位、十位、个位上的数字依次为a，b，c，当且仅当a＞b，b＜c时称为“凹数”（如213，312等），若a，b，c∈{1，2，3，4}，且a，b，c互不相同，则这个三位数为“凹数”的概率是．

答案解析收藏纠错 + 选题
16. (2023高二上·乐清开学考) 已知两个圆锥有公共底面，且两个圆锥的顶点和底面的圆周都在同一个球面上，若球的体积为 $\text{[math]}$ ，这两个圆锥的体积之和为 $\text{[math]}$ ，则这两个圆锥中，体积较大者的高与体积较小者的高的比值为.

答案解析收藏纠错 + 选题

四、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

17. (2023高二上·乐清开学考) 已知直线 $\text{[math]}$ 和 $\text{[math]}$ 的交点为 $\text{[math]}$ ．
1. （1）若直线 $\text{[math]}$ 经过点 $\text{[math]}$ 且与直线 $\text{[math]}$ 平行，求直线 $\text{[math]}$ 的方程；
2. （2）若直线 $\text{[math]}$ 经过点 $\text{[math]}$ 且与两坐标轴围成的三角形的面积为5，求直线 $\text{[math]}$ 的方程．
答案解析收藏纠错 + 选题
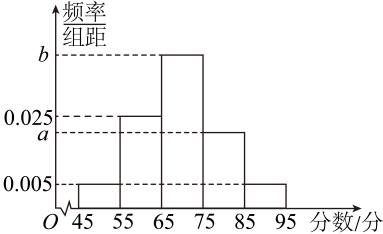
18. (2023高二上·乐清开学考) 为了迎接新高考，某校举行物理和化学等选科考试，其中，600名学生化学成绩（满分100分）的频率分布直方图如图所示，其中成绩分组区间是：第一组 $\text{[math]}$ ，第二组 $\text{[math]}$ ，第三组 $\text{[math]}$ ，第四组 $\text{[math]}$ ，第五组 $\text{[math]}$ .已知图中第三组频率为 $\text{[math]}$ ，第一组和第五组的频率相同.
1. （1）求a ， b的值；
2. （2）估算高分（大于等于80分）人数；
3. （3）估计这600名学生化学成绩的平均值（同一组中的数据用该组区间的中点值作代表）和中位数.（中位数精确到0.1）
答案解析收藏纠错 + 选题
19. (2023高二上·乐清开学考) 已知 $\text{[math]}$ 的内角A ， B ， C的对边分别为a ， b ， c ，且 $\text{[math]}$ .
1. （1）求角B大小；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的重心，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
20. (2023高二上·乐清开学考) 如图，四棱锥 $\text{[math]}$ 的底面是矩形， $\text{[math]}$ 底面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题
21. (2023高二上·乐清开学考) 已知圆 $\text{[math]}$ ，点P是直线 $\text{[math]}$ 上一动点，过点P作圆C的两条切线，切点分别为A ， B.
1. （1）若P的坐标为 $\text{[math]}$ ，求过点P的切线方程；
2. （2）直线 $\text{[math]}$ 与圆C交于E ， F两点，求 $\text{[math]}$ 的取值范围（O为坐标原点）.
答案解析收藏纠错 + 选题
22. (2023高二上·乐清开学考) 已知函数 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，判断函数 $\text{[math]}$ 的奇偶性（不需要给出证明）；
2. （2）若函数 $\text{[math]}$ 在 $\text{[math]}$ 上是增函数，求实数 $\text{[math]}$ 的取值范围；
3. （3）若存在实数 $\text{[math]}$ ，使得关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有三个不相等的实数根，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题