广东省阳江市江城区2023-2024学年八年级上学期数学期中...

更新时间：2023-12-19 浏览次数：23 类型：期中考试

一、选择题：本大题共10小题，每小题3分，共30分．在每小题列出的四个选项中，只有一项是符合题目要求的．

1. (2023八上·江城期中) 在以下绿色食品、节能、节水、可回收四个标志中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·江城期中) 现有两根木棒，它们的长分别为40 cm和60 cm，若要钉成一个三角形木架，则第三根木棒的长可以选取（）

A . 20cm B . 60 cm C . 100 cm D . 120 cm

答案解析收藏纠错 + 选题
3. (2023八上·江城期中) 以下图示能表示△ABC的边BC上的高的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023八上·江城期中) 一个多边形的内角和等于900°，则这个多边形的边数是（）

A . 5 B . 6 C . 7 D . 无法确定

答案解析收藏纠错 + 选题
5. (2023八上·江城期中) 如图，若△ABC≌△ADE，则下列结论一定成立的是（）

A . AC=DE B . ∠ABC=∠AED C . BC=AE D . ∠BAD=∠CAE

答案解析收藏纠错 + 选题
6. (2023八上·江城期中) 如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为α ，β，则下列正确的是（）

A . α-β=0 B . α-β<0 C . α-β>0 D . 无法比较α与β的大小

答案解析收藏纠错 + 选题
7. (2023八上·江城期中) 如图，在△ABC中，∠A=78°，∠ACD是△ABC的一个外角，∠EBC= $\text{[math]}$ ∠ABC，∠ECD= $\text{[math]}$ ∠ACD，则∠E的度数为（）

A . 22° B . 26° C . 28° D . 30°

答案解析收藏纠错 + 选题
8. (2023八上·江城期中) 如图，在△ABC中，AB=4，AC=5，以点A为圆心，任意长为半径画弧，分别交AB，AC于点D和E，再分别以点D，E为圆心，大于 $\text{[math]}$ DE长为半径画弧，两弧交于点F，连接AF并延长交BC于点M，作MN⊥AC于点N．若MN=2，则△ABM的面积为（）

A . 4 B . 5 C . 8 D . 10

答案解析收藏纠错 + 选题
9. (2023八上·江城期中) 图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（）

A . 90° B . 135° C . 150° D . 180°

答案解析收藏纠错 + 选题
10. (2023八上·江城期中) 如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，给出以下结论：①S_△_ABE= S_△B_CE；②∠AFG=∠AGF；③∠FAG=2∠ACF ；④BH=CH其中结论正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题：本大题共6小题，每小题3分，共18分．

11. (2022八上·鄯善月考) 桥梁搭桥，电视塔底座都是三角形结构，这是利用三角形的性．

答案解析收藏纠错 + 选题
12. (2023八上·江城期中) 点(- 2，1)关于 x轴对称的点的坐标为

答案解析收藏纠错 + 选题
13. (2023八上·江城期中) 如图，AE∥DF，AE=DF，要使△EAC≌△FDB，还需要添加的一个条件是(写出一种即可)

答案解析收藏纠错 + 选题
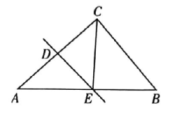
14. (2023八上·江城期中) 如图，在△ABC中，DE是AC的垂直平分线，分别交AC，AB于点D，E，若△BCE的周长为16，BC=6，则AB的长为

答案解析收藏纠错 + 选题
15. (2023八上·江城期中) 如图，在△ABC中，∠B=∠C=60°，BD=CF，BE=CD，那么∠EDF的度数是

答案解析收藏纠错 + 选题
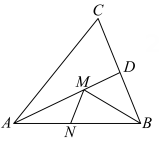
16. (2023八上·江城期中) 如图，在锐角三角形ABC中，AC=6，△ABC的面积为18，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM+MN的最小值是

答案解析收藏纠错 + 选题

三、解答题：本大题共9小题，共72分．解答应写出文字说明、证明过程或演算步骤．

17. (2023八上·江城期中) 在△ABC中，已知∠A=30°，∠B=2∠C，求∠B的度数．

答案解析收藏纠错 + 选题
18. (2023八上·江城期中) 如图，∠1=∠2，∠B=∠D，求证：AB=CD．

答案解析收藏纠错 + 选题
19. (2023八上·江城期中) 如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=34°，求∠DAE的度数．

答案解析收藏纠错 + 选题
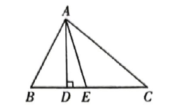
20. (2023八上·江城期中) 风筝起源于中国，至今已有2 300多年的历史．如题20图，在小明设计的”风筝”图案中，已知AB=AD，∠B=∠D，∠BAE=∠DAC．求证：AC=AE．

答案解析收藏纠错 + 选题
21. (2023八上·江城期中) 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为(0，-1)．
1. （1）请直接写出A，B两点的坐标；
2. （2）画出△ABC关于y轴对称的△A₁B₁C₁；
3. （3）求△ABC的面积．
答案解析收藏纠错 + 选题
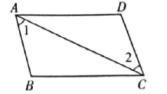
22. (2023八上·江城期中) 如图，已知∠A=∠D=90°，点E，F在线段BC上，DE与AF交于点O，且AB=DC，BE=CF．
1. （1）求证：AF=DE；
2. （2）若OP⊥EF，求证：OP平分∠EOF．
答案解析收藏纠错 + 选题
23. (2023八上·江城期中) 如图，在平面直角坐标系中，A(0，2)，B(1，0)，C(2，3)，CD⊥y轴于点D．
1. （1）求证：△AOB≌△CDA；
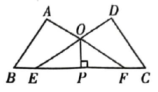
2. （2）连接BC，判断AB与CA的长度及位置的关系，并说明理由．
答案解析收藏纠错 + 选题
24. (2023八上·江城期中) [问题情境]
在综合实践课上，老师组织班上的同学开展了探究两角之间数量关系的数学活动，如题24图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点(与点A不重合)，BC，BD分别平分∠ABP和∠PBN，且分别交射线AM于点C，D．
[探索发现]
1. （1）当∠A=60°时，求证：∠CBD=∠A．
2. （2） ”快乐小组”经过探索后发现：不断改变∠A的度数，∠CBD与∠A始终存在某种数量关系．
  ①当∠A=40°时，∠CBD=度；
  ②当∠A=x°时，∠CBD=度(用含x的代数式表示)．
3. （3） [操作探究]
  ”智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变．请写出它们的关系，并说明理由．
答案解析收藏纠错 + 选题
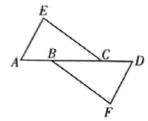
25. (2023八上·江城期中) 如图，AE与BD相交于点C，AC=EC，BC=DC，AB=4cm，点P从点A出发，沿A→B→A方向以3 cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P，Q两点同时出发．当点P到达点A时，P，Q两点同时停止运动．设点P的运动时间为t(s)．
1. （1）求证：AB∥DE；
2. （2）写出线段AP的长(用含t的式子表示)；
3. （3）连接PQ，当线段PQ经过点C时，求t的值．
答案解析收藏纠错 + 选题