贵州省黔东南州从江县东朗中学2023-2024学年八年级上学...

更新时间：2024-03-21 浏览次数：35 类型：期中考试

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2023八上·从江期中) 大自然中存在很多对称现象，下列植物叶子的图案中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·从江期中) 已知点P₁(a-1，5)和P₂(2，b-1)关于x轴对称，则(a+b)^{2 020}的值为（）

A . 0 B . -1 C . 1 D . (-3)^{2 019}

答案解析收藏纠错 + 选题
3. (2023八上·从江期中) 若一个三角形的三边长分别为3 cm，5 cm，a cm，则a的取值范围是（）

A . 3<a<5 B . 2<a<8 C . 3<a<8 D . 2<a<5

答案解析收藏纠错 + 选题
4. (2023八上·从江期中) 等腰三角形的两边长分别为6 cm和8 cm，则它的周长为（）

A . 20 cm B . 22 cm C . 20 cm或22 cm D . 18 cm，20 cm或22 cm

答案解析收藏纠错 + 选题
5. (2023八上·从江期中) 如图所示，已知AB=DC，下列条件中，不能判定△ABC≌△DCB的是（）

A . AC=DB B . ∠ACB=∠DBC C . ∠ABC=∠DCB D . ∠A=∠D=90°

答案解析收藏纠错 + 选题
6. (2023八上·从江期中) 下列说法：①三角形的内角中最多有一个钝角；②三角形的中线将三角形分成面积相等的两部分；③从n边形的一个顶点可以引(n-3)条对角线，把n边形分成(n-2)个三角形，因此，n边形的内角和是(n-2)·180°；④全等三角形的面积一定相等.正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. (2023八上·从江期中) 如图所示，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为（）

A . 30° B . 40° C . 70° D . 80°

答案解析收藏纠错 + 选题
8. (2023八上·从江期中) 如图所示，在△ABC中，∠C=90°，AE是△ABC的外角∠BAD的平分线，BF平分∠ABC与AE的反向延长线相交于点F，则∠BFE为（）

A . 35° B . 40° C . 45° D . 50°

答案解析收藏纠错 + 选题
9. (2023八上·从江期中) 如图所示，七边形ABCDEFG中，AB，ED的延长线相交于点O，若图中∠1，∠2，∠3，∠4的和为240°，则∠BOD的度数为（）

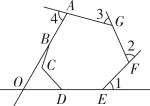
A . 40° B . 45° C . 50° D . 60°

答案解析收藏纠错 + 选题
10. (2023八上·从江期中) 如图所示，把长方形纸片ABCD沿对角线所在直线折叠，设重叠部分为△EBD，那么下列说法错误的是（）

A . △EBD是等腰三角形，EB=ED B . 折叠后∠ABE和∠EBD一定相等 C . 折叠后得到的图形是轴对称图形 D . △EBA和△EDC′一定是全等三角形

答案解析收藏纠错 + 选题
11. (2023八上·从江期中) 如图所示，∠AOB=α，点P是∠AOB内的一定点，点M，N分别在OA，OB上移动，当△PMN的周长最小时，∠MPN的值为（）

A . 90°+α B . 90°+ $\text{[math]}$ α C . 180°-α D . 180°-2α

答案解析收藏纠错 + 选题
12. (2023八上·从江期中) 如图所示，在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：
①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC.其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2024八上·南昌期中) 在Rt△ABC中，∠C=90°.若∠A=37°，则∠B的度数为.

答案解析收藏纠错 + 选题
14. (2023八上·从江期中) 如图所示，在Rt△ABC中，∠ACB=90°，∠A=20°，△ABC≌△A′B′C，若A′B′恰好经过点B，A′C交AB于点D，则∠BDC的度数为.

答案解析收藏纠错 + 选题
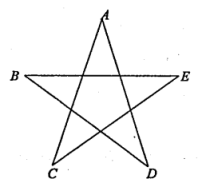
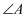
15. (2023八上·从江期中) 某校用红色灯带制作了一个如图所示的正五角星（A、B、C、D、E是正五边形的五个顶点），则图中 $\text{[math]}$ 的度数是度．

答案解析收藏纠错 + 选题
16. (2023八上·从江期中) 给出如下定义：点P是△ABC内部一点，如果存在过点P的直线可以将△ABC分成面积相等的两部分，则称该点为△ABC的“中立点”，下列四个结论中：
①当点P在△ABC的一条中线上时，该点为△ABC的“中立点”；
②△ABC的“中立点”的个数为有限个；
③△ABC的“中立点”有无数个，但不是△ABC内部所有的点；
④△ABC内部所有的点都是△ABC的“中立点”.
所有正确结论的序号是.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2023八上·从江期中) 如图所示，AD是△ABC的角平分线，BE是△ABD的高，
∠ABC=40°，∠C=80°.求∠EBD的度数.

答案解析收藏纠错 + 选题
18. (2023八上·从江期中) 在平面直角坐标系中，△ABC的三个顶点的位置如图所示.
1. （1）若△ABC内有一点P(a，b)随着△ABC平移后到了点P′(a+4，b-1)，直接写出A点平移后对应点A′的坐标；
2. （2）直接作出△ABC关于y轴对称的△A′B′C′(其中A′，B′，C′分别是A，B，C的对应点)；
3. （3）求四边形ABC′C的面积.
答案解析收藏纠错 + 选题
19. (2023八上·从江期中) 如图所示，在△ABC中.
1. （1）作△ABC的中线CD(尺规作图，不写作法，保留作图痕迹).
2. （2）若CD=AD，求∠ACB的度数.
答案解析收藏纠错 + 选题
20. (2023八上·从江期中) 如图所示，一艘轮船以40 n mile/h的速度沿正北方向航行，在A处测得灯塔C在北偏西30°方向上，轮船航行2 h后到达B处，在B处测得灯塔C在北偏西60°方向上.轮船又航行了多远到达灯塔C的正东方向D处?

答案解析收藏纠错 + 选题
21. (2023八上·从江期中) 如图所示，要测量河两岸上A，B两点的距离，在点B的河岸一侧平地上取一点C，连接BC，并延长BC到点D，使CD=BC，画出∠CDF=∠ABC.在射线DF上取点E，使E，A，C在一条直线上，这时测得DE的长就是A，B两点的距离.为什么?

答案解析收藏纠错 + 选题
22. (2023八上·从江期中) 如图所示，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB.
1. （1）若∠ABC=70°，则∠NMA的度数是.
2. （2）若AB=8 cm，△MBC的周长是14 cm.
  ①求BC的长度；
  ②若点P为直线MN上一点，请你直接写出△PBC周长的最小值.
答案解析收藏纠错 + 选题
23. (2023八上·从江期中) 在△ABC中，∠ACB=90°，∠A=30°，BC=4，点D是AB边上一动点，过点D作DE⊥AB，交AC于点E，将△AED沿直线DE翻折，使点A落在AB边上的点F处，连接CF.当△FEC是直角三角形时，求出AD的长.

答案解析收藏纠错 + 选题
24. (2023八上·从江期中) 如图所示，在△ABC中，∠B=∠C，AB=8 cm，BC=6 cm，点D为AB的中点.如果点P在线段BC上以 2 cm/s的速度由B点向C点运动，同时，点Q在线段CA上以 a cm/s 的速度由C点向A点运动，设运动时间为t(s)(0≤t≤3).
1. （1）用含t的代数式表示PC的长度；
2. （2）若点P，Q的运动速度相等，经过1 s后，△BPD与△CQP是否全等，请说明理由；
3. （3）若点P，Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等?
答案解析收藏纠错 + 选题
25. (2023八上·从江期中) 某数学兴趣小组在活动时，老师提出了这样一个问题：如图(1)所示，在△ABC中，AB=6，AC=8，D是BC的中点，求BC边上的中线AD的取值范围.
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，请补充完整证明“△ABD≌△ECD”的推理过程.
1. （1）求证：△ABD≌△ECD；
  证明：延长AD到点E，使DE=AD，
  在△ABD和△ECD中，
  ∵AD=ED(已作)，
  ∠ADB=∠EDC(▲ )，
  CD= ▲ (线段中点的定义).
  ∴△ABD≌△ECD(▲ ).
2. （2）由(1)的结论，根据AD与AE之间的关系，探究得出AD的取值范围是 ▲ ；
3. （3）【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中.
  【问题解决】如图(2)中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长.
答案解析收藏纠错 + 选题