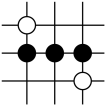
 B .
B . 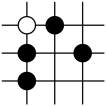 C .
C . 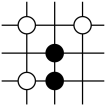 D .
D . 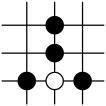
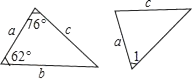


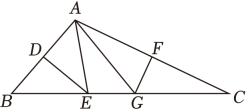

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ;
②当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ;
③当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ;
其中所有正确结论的序号是 .
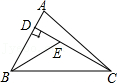
已知:如图,在Rt△ABC中,∠ABC=90°,
求作:点D , 使点D在BC边上,且到AB和AC的距离相等.
作法:①如图,以点A为圆心,任意长为半径画弧,分别交AB , AC于点M、N;
②分别以点M , N为圆心,大于![]() MN的长为半径画弧,两弧交于点P;
MN的长为半径画弧,两弧交于点P;
③画射线AP , 交BC于点D .
所以点D即为所求.
根据小东设计的尺规作图过程:
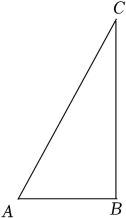
证明:过点D作DE⊥AC于点E , 连接MP , NP .
在△AMP与△ANP中,
∵AM=AN , MP=NP , AP=AP ,
∴△AMP≌△ANP(SSS).
∴∠▲=∠▲ .
∵∠ABC=90°,
∴DB⊥AB .
又∵DE⊥AC ,
∴DB=DE( )(填推理的依据)
