广东省茂名市博雅中学2023-2024学年九年级上学期数学期...

更新时间：2024-01-28 浏览次数：18 类型：期中考试

一、单选题（本大题共10小题，每小题3分，共30分）

1. (2023九上·茂名期中) 下列方程为一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·茂名期中) 若两个相似三角形的相似比为 $\text{[math]}$ ，则这两个三角形的周长之比为（）

A . $\text{[math]}$ B . 1：9 C . 1：27 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·茂名期中) 如图，公路 $\text{[math]}$ 互相垂直，公路 $\text{[math]}$ 的中点 $\text{[math]}$ 与点 $\text{[math]}$ 被湖隔开，若测得 $\text{[math]}$ 的长为 $\text{[math]}$ ，则 $\text{[math]}$ 两点间的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·茂名期中) 不透明的袋子中装有红、蓝小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，两次都摸到相同颜色的小球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·龙岗月考) 用配方法解方程 $\text{[math]}$ 时，原方程应变形为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·茂名期中) 顺次连接矩形各边中点得到的四边形是（）

A . 梯形 B . 矩形 C . 菱形 D . 正方形

答案解析收藏纠错 + 选题
7. (2023九上·茂名期中) 如图， $\text{[math]}$ 是正方形 $\text{[math]}$ 的边 $\text{[math]}$ 延长线上的一点，且 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·扶风期中) 在第十九届亚运会中国国家象棋队选拔赛的第一阶段中，采用分组单循环（每两人之间都只进行一场比赛）制，每组 $\text{[math]}$ 人，若每组共需进行15场比赛，则根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·茂名期中) 如图所示，点 $\text{[math]}$ 是 $\text{[math]}$ 的边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以下条件中，不能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·茂名期中) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一动点，过点 $\text{[math]}$ 分别作 $\text{[math]}$ 于点 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 2 B . 2.4 C . 2.5 D . 3

答案解析收藏纠错 + 选题

二、填空题（本大题6小题，每小题4分，共24分）

11. (2023九上·茂名期中) 一元二次方程 $\text{[math]}$ 的二次项系数，一次项系数.

答案解析收藏纠错 + 选题
12. (2023九上·茂名期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值等于.

答案解析收藏纠错 + 选题
13. (2023九上·茂名期中) 如图， $\text{[math]}$ ，直线 $\text{[math]}$ 与这三条平行线分别交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是.

答案解析收藏纠错 + 选题
14. (2023九上·茂名期中) 在一个不透明的袋子中有红球和白球共20个，它们除颜色外都相同，每次从袋中随机摸出一个小球，记下颜色后再放回袋中，通过多次重复实验，发现摸出白球的频率稳定在0.7附近，则估计袋子中的白球有个.

答案解析收藏纠错 + 选题
15. (2023九上·茂名期中) 等腰三角形的两条边长分别是方程 $\text{[math]}$ 的两根，则该等腰三角形的周长是.

答案解析收藏纠错 + 选题
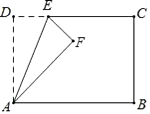
16. (2023九上·茂名期中) 如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为．

答案解析收藏纠错 + 选题

三、解答题（一）（本大题3小题，每小题6分，共18分）

17. (2023九上·茂名期中) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2023九上·茂名期中) 2022年东奥会在北京举办.现有如图所示“2022·北京冬梦之约”的四枚邮票供小明选择，依次记为 $\text{[math]}$ ，背面完全相同.将这四枚邮票背面朝上，洗匀放好.
1. （1）小明从中随机抽取一枚，恰好抽到是 $\text{[math]}$ （冰墽墩）概率是（直接写出结果）.
2. （2）小颖从中随机抽取一枚不放回，再从中随机抽取一枚.请用列表或画树状图的方法，求小颖同学抽到的两枚邮票恰好是 $\text{[math]}$ （冰墩墩）和 $\text{[math]}$ （雪容融）的概率.
答案解析收藏纠错 + 选题
19. (2023九上·茂名期中) 小强在地面 $\text{[math]}$ 处放一面镜子，刚好能从镜子中看到教学楼的顶端 $\text{[math]}$ ，此时 $\text{[math]}$ 米， $\text{[math]}$ 米.已知眼睛距离地面的高度 $\text{[math]}$ 米，请计算出教学楼 $\text{[math]}$ 的高度.（根据光的反射定律，反射角等于入射角）

答案解析收藏纠错 + 选题

四、解答题（二）（本大题3小题，每小题7分，共21分）

20. (2023九上·茂名期中) 菱形 $\text{[math]}$ 的对角线 $\text{[math]}$ 长 $\text{[math]}$ ，周长是 $\text{[math]}$ .求：
1. （1）对角线 $\text{[math]}$ 的长度；
2. （2）菱形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
21. (2023九上·茂名期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，延长 $\text{[math]}$ 至 $\text{[math]}$ ，使得 $\text{[math]}$ ，过点 $\text{[math]}$ 分别作 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ .下面是两位同学的对话：
小星：由题目的已知条件，若连接 $\text{[math]}$ ，则可证明 $\text{[math]}$ .
小红：由题目的已知条件，若连接 $\text{[math]}$ ，则可证明 $\text{[math]}$ .
1. （1）请你选择一位同学的说法，并进行证明；
2. （2）连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，试判断 $\text{[math]}$ 与 $\text{[math]}$ 有怎样的关系，并证明你的结论.
答案解析收藏纠错 + 选题
22. (2023九上·茂名期中) 某水果商场销售一种高档水果.
1. （1）若原售价每千克50元，连续两次降价后为每千克32元，已知每次下降的百分率相同，求每次下降的百分率；
2. （2）若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且尽可能减轻顾客负担，那么每千克应涨价多少元？
答案解析收藏纠错 + 选题

五、解答题（三）（本大题3小题，每小题9分，共27分）

23. (2023九上·茂名期中) 如图，在平行四边形 $\text{[math]}$ 中，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ 为线段 $\text{[math]}$ 上一点，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
24. (2023九上·茂名期中) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ 是方程的一个根，求 $\text{[math]}$ 的值和方程的另一根；
2. （2）当 $\text{[math]}$ 为何实数时，方程有实数根；
3. （3）若 $\text{[math]}$ 是方程 $\text{[math]}$ 的两个根，阅读材料：设一元二次方程 $\text{[math]}$ 的两根为 $\text{[math]}$ ，则两根与方程系数之间有如下关系： $\text{[math]}$ .根据该材料且 $\text{[math]}$ ，试求实数 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2023九上·茂名期中)
1. （1）【问题探究】
  如图（1）在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上的点， $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上的点，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为.
2. （2）【类比迁移】
  如图（2）在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ ，过 $\text{[math]}$ 的中点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的长度.
3. （3）【拓展应用】
  如图（3）李大爷家有一块平行四边形 $\text{[math]}$ 的菜地，测得 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ ，为了管理方便，李大爷沿着对角线 $\text{[math]}$ 开一条小路，过这小路的正中间，开了另一条垂直于它的小路 $\text{[math]}$ （小路面积忽略不计），求新开出的小路 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题