广东省清远市清新区2023-2024学年八年级上学期数学期中...

更新时间：2024-02-26 浏览次数：12 类型：期中考试

一、选择题（本大题共10小题，每小题3分，共30分）

1. (2021八上·佛山期中) 下列数中，无理数的是（　　）

A . π B . $\text{[math]}$ C . $\text{[math]}$ D . 3.1415926

答案解析收藏纠错 + 选题
2. (2022八下·上林期末) 在圆的面积公式S＝πR²中，变量是（　　）

A . S、π、R B . S、R C . π、R D . 只有R

答案解析收藏纠错 + 选题
3. (2022八下·娄星期末) 下列函数中，是一次函数的是（）

A . $\text{[math]}$ B . y=3x+1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021七下·会昌期末) 点A（﹣1，2）到x轴的距离是（）

A . ﹣1 B . 1 C . ﹣2 D . 2

答案解析收藏纠错 + 选题
5. 如图，阴影部分的四边形均为正方形，图中的数据表示其面积，则正方形M的面积为（）

A . 1 B . 7 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
6. 如图，数轴上点A对应的数是0，点C对应的数是-4，BC⊥AC ，垂足为C ，且BC＝1，以点A为圆心，AB长为半径画弧，交数轴于点D ，则点D表示的数为（）

A . - $\text{[math]}$ B . $\text{[math]}$ C . -4.2 D . -4.5

答案解析收藏纠错 + 选题
7. 两个变量y与x之间的关系如图所示，那么y随x的增大而（）

A . 增大 B . 减小 C . 不变 D . 有时增大有时减小

答案解析收藏纠错 + 选题
8. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 下列语句正确的是（）

A . a的平方根是 $\text{[math]}$ （a≥0） B . 在同一平面内，垂直于同一条直线的两直线平行 C . 同旁内角互补 D . 若ab＝0，则点P（a ， b）在坐标原点

答案解析收藏纠错 + 选题
10. 如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形，若直角三角形的两条直角边长分别为a ， b（a＞b），大正方形的面积为S₁ ，小正方形的面积为S₂ ，则用含S₁ ， S₂的代数式表示（a+b）²正确的是（）

A . S₁ B . S₂ C . 2S₁-S₂ D . 2S₂-S₁

答案解析收藏纠错 + 选题

二、填空题（共5小题，满分15分，每小题3分）

11. (2018八上·顺义期末) 25的平方根是 .

答案解析收藏纠错 + 选题
12. (2019八上·房山期中) 比较大小： $\text{[math]}$ $\text{[math]}$ ．（填“＞、＜、或=”）

答案解析收藏纠错 + 选题
13. 已知 $\text{[math]}$ 是方程组 $\text{[math]}$ 的解，则a+b＝．

答案解析收藏纠错 + 选题
14. 定义新运算※，对于任意实数a ， b都有a※b＝a²+ab ，如果3※4＝3²+3×4＝9+12＝21，那么方程x※5＝0的解为．

答案解析收藏纠错 + 选题
15. 如图，在直角坐标系中，点A、B的坐标分别为（1，3）和（4，0），点C是y轴上的一个动点，当|BC-AC|最大时，点C的坐标是．

答案解析收藏纠错 + 选题

三、解答题（共8小题，满分75分）

16. 小明和同桌小聪在课后复习时，对练习册“目标与评定”中的一道思考题，进行了认真地探索．（思考题）如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？

答案解析收藏纠错 + 选题
17. 计算
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18.
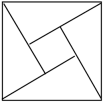
⑴如图4×4的方格，每个小格的顶点叫做格点，若每个小正方形边长为1单位，请在方格中作一个正方形，同时满足下列两个条件：
①所作的正方形的顶点，必须在方格上；
②所作正方形的面积为8个平方单位
⑵在数轴上表示实数 $\text{[math]}$ （保留作图痕迹）

答案解析收藏纠错 + 选题
19. (2023八下·江油月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，分别求下列代数式的值：
1. （1） a²-b²；
2. （2） a²-2ab+b² ．
答案解析收藏纠错 + 选题
20. 如图，销售某产品，l₁表示一天的销售收入y₁（万元）与销售量x（件）的关系l₂表示一天的销售成本y₂（万元）与销售量x的关系．
1. （1） y₁与x的函数关系式；y₂与x的函数关系式；
2. （2）每天的销售量达到多少件时，每天的利润达到18万元？
答案解析收藏纠错 + 选题
21. 综合与实践
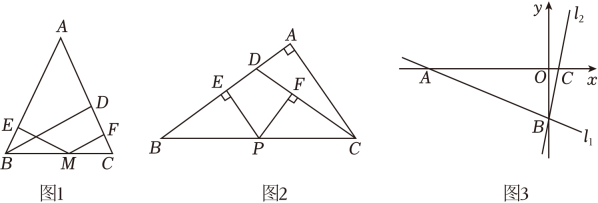
问题情境：某消防队在一次应急演练中，消防员架起一架长25m的云梯AB ，如图，云梯斜靠在一面墙上，这时云梯底端距墙脚的距离BC＝7m ， ∠DCE＝90°．
1. （1）独立思考：
  这架云梯顶端距地面的距离AC有多高？
2. （2）深入探究：
  消防员接到命令，按要求将云梯从顶端A下滑到A′位置上（云梯长度不改变），AA′＝4m ，那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗？若是，请说明理由；若不是，请求出BB′的长度．
3. （3）问题解决：
  在演练中，高24.3m的墙头有求救声，消防员需调整云梯去救援被困人员．经验表明，云梯靠墙摆放时，如果云梯底端离墙的距离不小于云梯长度的 $\text{[math]}$ ，则云梯和消防员相对安全．在相对安全的前提下，云梯的顶端能否到达24.3m高的墙头去救援被困人员？
答案解析收藏纠错 + 选题
22. 已知，正六边形ABCDEF ，边长为6，G点以每秒为1的速度从A→B→C→D→E上运动，不与E点重合，同时，点H以同样的速度从B→C→D→E→F上运动，不与F点重合，连接GF、AH交于点I；
1. （1）求∠E的度数．
2. （2）如图1，IJ是∠FIH的角平分线，过F点作IJ的垂线，垂足为J ，当FI是∠AFJ的角平分线时，求证AI＝IJ ．
3. （3）如图2，过B点作FG的平行线，交直线AH于点L ，当G在运动的过程中，写出FI、AL、AI之间的数量关系，并给出证明．
答案解析收藏纠错 + 选题
23. 学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为等面积法．
1. （1）【学有所用】如图1，在等腰△ABC中，AB＝AC ，其一腰上的高BD为h ， M是底边BC上的任意一点，M到腰AB、AC的距离ME、MF分别为h₁、h₂ ，小明发现，通过连接AM ，将△ABC的面积转化为△ABM和△ACM的面积之和，建立等量关系，便可证明h₁+h₂＝h ，请你结合图形来证明：h₁+h₂＝h；
2. （2）【尝试提升】如图2，在△ABC中，∠A＝90°，D是AB边上一点，使BD＝CD ，过BC上一点P ，作PE⊥AB ，垂足为点E ，作PF⊥CD ，垂足为点F ，已知AB＝6 $\text{[math]}$ ， BC＝6 $\text{[math]}$ ，求PE+PF的长．
3. （3）【拓展迁移】如图3，在平面直角坐标系中有两条直线l₁：y＝- $\text{[math]}$ x-5，l₂：y＝5x-5，若l₂上的一点M到l₁的距离是2，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题